Trigonometría plana -conceptos básicos
Trigonometría: es la rama de la Matemática que se encarga del estudio de las relaciones numéricas entre los elementos que forman los triángulos planos o esféricos.
De modo que se puede distinguir dos tipos de trigonometría, la plana y la esférica. Este apartado trata solamente de trigonometría plana.
Para iniciar el estudio de la trigonometría conviene recordar algunos conceptos importantes de la geometría, a continuación, se presentan aquellos considerado de mayor utilidad para los fines.
Ángulo y medidas de ángulos.
Se dice que un ángulo es la intersección de dos semirectas en un punto llamado vértice.
Si el ángulo tiene un sentido de giro contrario a las agujas del reloj se dice que el ángulo es positivo. Si tiene un sentido de giro según las agujas del reloj el ángulo es negativo.
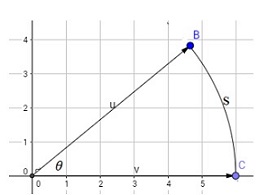
En la figura de la izquierda se presenta un ángulo en posición normal (vértice en el punto \((0,0)\) y sentido de giro positivo), formado por las semirectas \({\rm u}\) y \({\rm v} \) el cual posee una longitud de arco \(s\).
Nota. Un ángulo no necesariamente debe estar en posición normal, en la práctica los ángulos adoptan muchas posiciones según sea la situación estudiada.
Se suelen nombrar los ángulos con una letra mayúscula, o con tres letras que representan los lados y el vértice, por ejemplo, en la figura anterior el ángulo theta es \(\theta=BOC\) donde la letra del centro indica el vértice. Además, si dos ángulos en posición normal tienen los mismos lados terminales, se dice que son ángulos coterminales.
Medida de ángulos.
Las dos maneras más comunes de medir un ángulo son los grados y radianes (unidad de medida de ángulo del Sistema Internacional).
Un grado es el equivalente a una trecientos sesentava parte de una revolución completa alrededor del del vértice \(1°=1 \rm{vuelta}/360°.\) Dado que la trayectoria de un cuerpo cuando completa una vuelta es una circunferencia, se dice que un grado es una trecientos sesentava parte de una circunferencia, de modo que una vuelta es equivalente a 360 grados lo cual se escribe \(1 \rm vuelta=360°\).
Otra manera de medir los ángulos es en radianes, un radian se define como la medida de un ángulo central de una circunferencia de radio \(r\) cuya longitud del arco \(s\) comprendido entre los rayos es igual a la longitud del radio.
Algebraicamente cuando se mide en radianes la longitud de arco \(s=r\theta\). Dado que la longitud (perímetro) de una circunferencia es \(s=2\pi r\) se tiene que una \(1 {\rm vuelta}=2\pi r\). De donde un ángulo central de una revolución completa alrededor del vértice en sentido contrario a las agujas del reloj describe una trayectoria que mide \(2\pi r\) por tanto, se tiene que \(1 {\rm vuelta}=2\pi r=2\pi\) radianes.
Equivalencia entre grados y radianes:
$$1 {\rm vuelta}=360°=2π~~rad⟹180°=π rad$$
Ver los ejemplos Ej1 y Ej2 del apartado Ejercicios I.
Clasificación de ángulos según sus medidas.
Según la medida de un ángulo, al medir en grados, estos se pueden clasificar en:
Agudos: miden más de cero, pero menos de noventa grados.
Rectos: miden exactamente noventa grados (lados perpendiculares entre sí)
Obtuso: miden más de noventa grados, pero menos de \(180°\).
Llanos. miden exactamente \(180°\)
Completos: miden \(360°\) y coinciden con el ángulo nulo \(0°\).
Además, se dice que dos ángulos son complementarios si la suma de sus medidas es noventa grados y son suplementarios si la suma de sus medidas es \(180°\). Ver los ejemplos Ej2 y Ej3 de los Ejercicios I.
Funciones trigonométricas de ángulos agudos.
Para comenzar el estudio de las funciones trigonométricas recuerde que un triángulo es rectángulo si dos de sus lados son perpendiculares entre sí, y por consecuencia tiene exactamente un ángulo recto.
El lado más grande del triángulo es llamado hipotenusa y los otros dos son llamados catetos. Cuando se mide en grados el ángulo opuesto a la hipotenusa es un ángulo recto (sus lados son perpendiculares) y en consecuencia mide exactamente \(90°\). Los ángulos restante del triangulo son ángulos agudos y además complementarios (la suma de sus medidas es noventa grados).
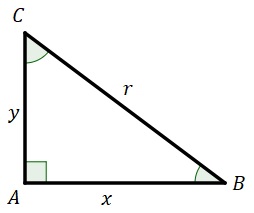
Lado opuesto a un ángulo en un triángulo: es el lado ubicado enfrente del ángulo. Por ejemplo, el lado \(x\) es opuesto al \(\angle{C}.\)
Lado adyacente a un ángulo en un triángulo: es el lado continuo (pegado) al ángulo en el triángulo. Por ejemplo, el lado \(y\) es adyacente al ángulo \(\angle C.\)
En todo triángulo rectángulo se cumple el teorema de Pitágoras el cual relaciona las medidas de las longitudes de sus lados mediante la expresión \(r^2=x^2+y^2\) la cual resulta de gran utilidad al estudiar trigonometría.
Otro elemento a recordar es que un ángulo \(\theta\) es agudo si al medir en grado su medida es mayor que cero, pero menor que noventa, esto es \(0° \leq\theta\leq90°\), para tales ángulos se definen las funciones trigonométricas como sigue:
\(1\). Seno de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud del lado opuesto y la longitud de la hipotenusa.
\(2\). Coseno de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud del lado adyacente y la longitud de la hipotenusa.
\(3\). Tangente de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud del lado opuesto y la longitud del lado adyacente.
\(4\). Cotangente de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud del lado adyacente y la longitud del lado opuesto a este.
\(5\). Secante de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud de la hipotenusa y la longitud del lado adyacente. Es decir, es el reciproco del coseno de dicho ángulo.
\(6\). Cosecante de un ángulo agudo: en un triángulo rectángulo se define como la razón proporcional entre la longitud de la hipotenusa y la longitud del lado opuesto. La función cosecante es la reciproca del seno de dicho ángulo.
Funciones trigonométricas del ángulo \(u\)
\begin{array} {l l} {\rm Función}& {\rm Notación}\\ {\rm Seno}&\sin{u}\\ {\rm Coseno}&\cos{u}\\ {\rm Tagente}&\tan{u}\\ {\rm Cotangente}&\cot{u}\\ {\rm Secante}&\sec{u}\\ {\rm Cosecante}&\csc{u}\\ \end{array} Ver Ej5, Ej6 y Ej7 de los Ejercicios I.
Funciones trigonometricas de ángulos complementarios
Se dice que dos ángulos phi (\(\phi\)) y theta (\(\theta\)) son complementarios cuando la suma de sus medidas al medir en grados es \(180°\) (si se mide en radianes entonces es \(\pi/2\)), y para tales ángulos se cumple el siguiente teorema.
Funciones trigonometricas de ángulos complementarios
Si dos ángulos son complementarios, los valores de las funciones de uno, son los valores de las cofunciones de su complemento y viceversa.
Ver Ej7 y Ej8 de los Ejercicios I.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Trigonometría de ángulos notables.
Para ciertos ángulos considerados como ángulos notables, \(30°,45°,60°\) y los ángulos de \(0°,90°,180°,270°\) y \(360°\) los cuales se ubican sobre los ejes de coordenadas en posición normal (llamados ángulos cuadrantales) la determinación de los valores de las funciones trigonométricas está dada por la geometría plana en la manera siguiente.
Funciones trigonométricas de \(30°\) y \(60°\)
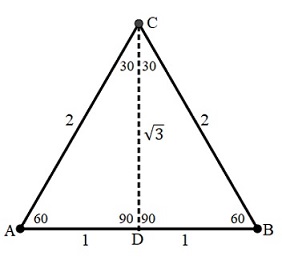Partiendo de un triángulo equilátero en el cual por comodidad se trazan lados de lóngitud \(l=2\) (escrita sin unidades de medida por ser irrelevante), entonces se pueden determinar los valores de las funciones trigonométricas de 30° y 60° como se muestra a continuación.
Como construcción auxiliar, en el triángulo \(ABC\) se muestra el segmento \(\overline{CD}\) que por ser el triángulo equilátero es bisectriz, mediatriz, mediana y altura, del teorema de Pitágoras \(\overline{CD}=\sqrt3\). Debidio a que el valor de las funciones trigonométricas carece de unidad de medida, solo es necesario escribir los números.
Funciones trigonométricas de 30° \begin{align} &\sin{30°}=\frac{\rm c.op}{h}=\frac{1}{2}\\ &\cos{30°}=\frac{\rm c.ady}{h}=\frac{\sqrt{3}}{2}\\ &\tan{30°}=\frac{\rm c.op}{\rm c.ady}=\frac{1}{\sqrt3} =\frac{\sqrt3}3\\ &\cot{30°}=\frac{\rm c.ady}{\rm c.op}=\frac{\sqrt3}{1}=\sqrt3\\ &\sec{30°}=\frac{h}{\rm c.ady}=\frac{2}{\sqrt3} =\frac{2\sqrt3}{3}\\ &\csc{30°}=\frac{h}{\rm c.op}=\frac21=2\\ \end{align}
Funciones trigonométricas de \(60°\)
Los valores de las funciones trigonométricas de \(60°\) se obtienen realizando un análisis homólogo, tomando como referencia el ángulo A o el ángulo B de la figura, o por medio del uso del teorema para funciones trigonométricas de ángulos complementarios.
\begin{align}
&\sin{60°}=\frac{\rm c.op}{h}=\frac{\sqrt{3}}{2}= \frac{\sqrt3}{2}\\
&\cos{60°}=\frac{\rm c.ady}{h}=\frac{1}{2}=\frac12\\
&\tan{60°}=\frac{\rm c.op}{\rm c.ady}=\frac{\sqrt3}{1}=\sqrt3\\
&\cot{60°}=\frac{\rm c.ady}{\rm c.op}=\frac{1}{\sqrt3} =\frac{\sqrt3}3\\
&\sec{60°}=\frac{h}{\rm c.ady}=\frac{2}{\sqrt3} =\frac21=2\\
&\csc{60°}=\frac{h}{\rm c.op}=\frac{2\sqrt3}{3}\\
\end{align}
Funciones trigonométricas de \(45°\)
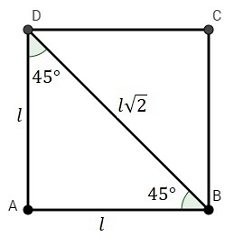
Para las funciones trigonométricas de \(45°\) se parte de un cuadrado de longitud de lado igual a \(l\), trazando una diagonal, que por ser un cuadrado es bisectriz quedando así determinada la figura de la izquierda de donde,
\begin{align} &\sin{45°}=\frac{c.op}{h}=\frac{l}{l\sqrt2}=\frac{\sqrt2}2\\ &\csc{45°}=\frac{h}{c.op}=\frac{l\sqrt2}{l}=\sqrt2\\ &\cos{45°}=\frac{c.ady}{h}=\frac{l}{l\sqrt2}=\frac{\sqrt2}2\\ &\sec{45°}=\frac{h}{c.ady}=\frac{l\sqrt2}{l}=\sqrt2\\ &\tan{45°}=\frac{c.op}{c.ady}=\frac{l}l=1\\ &\cot{45°}=\frac{c.ady}{c.op}=\frac{l}l=1\\ \end{align}
Algunos autores además de esto ángulos, consideran como ángulos notables a aquellos ángulos formados en un triángulo rectángulo cuyas longitudes de sus lados forman una terna pitagóri-ca, a continuación, el ejemplo más simple de este caso.
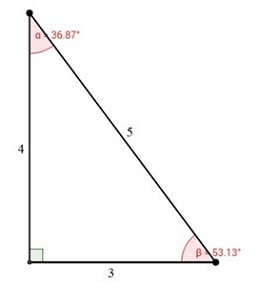Note de la figura de la izquierda que los valores de los ángulos alfa y beta no corresponden a valores exactos (están redondeados a la centésima) para tener \(\alpha=36.87°\) y \( \beta=53.13°\), así que lo que presentan estos autores es una aproximación en la cual los ángulos alfa y beta son redondeados aún más haciendo \(\alpha=37°\) y \(\beta=53°\), bajo este redondeo se escriben las funciones trigonométricas para estos ángulos con los valores siguientes.\begin{array}1
\sin{\alpha}=3/5=\cos{\beta} &
\csc{\alpha}=5/3=\sec{\beta}\\
\cos{\alpha}=4/5=\sin{\beta}
&\sec{\alpha}=5/4=\csc{\beta}\\
\tan{\alpha}=3/4=\cot{\beta}
&\cot{\alpha}=4/3=\tan{\beta}\end{array}
Esta idea, aunque carece de la “exactitud matemática” por ser una aproximación, no es del todo descabellada, ya que al comparar los valores exactos de las funciones para \(\alpha=37°\) y \(\beta=53°\) el error mayor que se encuentra es aproximadamente tres milésimas. Así que en aquellos casos no científicos en los cuales no se requiera la exactitud se pueden asumir estos valores.
Funciones de ángulos de coterminales.
Se dice que dos ángulos son coterminales (que terminan en el mismo punto) cuando uno de ellos es el otro aunmentado en \(n360°\) o \(2n\pi \rm rad\) donde \(n\) es un entero distinto de cero. Así por ejemplo un angulo de \(390°\) es coterminal con un ángulo de treinta grados ya que \(390°=30°+360°\). La importancia de esta afirmación en trigonometría radica en que los angulos coterminales tienen las mismas funciones trigonometricas.
Ángulos de referencias y funciones trigonométrica
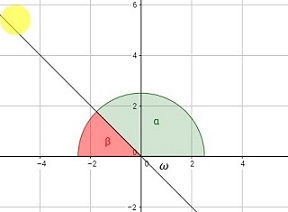Sea alpha \((\alpha)\) un ángulo en posición normal (vértice en \((0,0)\) y sentido de giro positivo), luego el ángulo de referencia beta \((\beta)\) relacionado con \(\alpha,\) es el ángulo formado por el lado terminal de Alpha y el eje de abscisas (normalmente el eje \(x\)).
En la figura de arriba se observa el ángulo \(\alpha\) al cual corresponde el ángulo de referencia \(\beta.\)
La importancia que poseen los ángulos de referencias en la trigonometría radica en que, obviando los signos, las funciones trigonométricas del ángulo de referencia beta, son las mismas funciones trigonométricas del ángulo alpha, de donde basta tener en cuenta los signos de las funciones trigonométricas del ángulo beta, para escribirlas en función de alfa.
Por ejemplo, suponiendo un ángulo \(\alpha=135°\) que se ubica como en la figura de arriba. El ángulo de referencia \(\beta=45°\) por ser \(\alpha\) y \(\beta\) dos angulos complemetarios, de donde las funciones trigonométricas del ángulo \(\alpha\) son como sigue.
\begin{align}
\sin135°&=\sin45°=\frac{\sqrt2}2\\
\cos135°&=-\cos45°=-\frac{\sqrt2}2 ~~~~~~~~\mathrm{Por~ ser~} x~ \mathrm{ negativa.}\\
\tan135°&=-\tan45°=-1 ~~~~~~~~~~~~~\mathrm{Por~ ser~} x~ \mathrm{ negativa.}\\
\cot135°&=-\cot45°=-1~~~~~~~~~~~~~~\mathrm{Por~ ser~} x~ \mathrm{ negativa.}\\
\sec135°&=-\sec45°=-2 ~~~~~~~~~~~~~~\mathrm{Por~ ser~} x~ \mathrm{ negativa.}\\
\csc135°&=\csc45°=2
\end{align}
Más aun, beta \(\beta\) y omega \(\omega\) son congruentes (por ser opuestos por el vértice) y por tanto, tienen igual medida, de esto teniendo en cuenta los signos, se pueden escribir las funciones para el ángulo \(\theta=360°-\omega\) que está en el cuarto cuadrante, tomando a \(\omega\) como ángulo de referencia.
Así para un ángulo phi \(\phi\) medido desde el eje \(x\) positivo hasta el lado terminal de omega \(\omega\), considerando solo su valor \(\omega=45°\) e ingnorando su posición), las funciones de este ángulo \(\phi\) del cuarto cuadrante están dadas por \(\phi=360°-\omega\Longrightarrow \phi=315\) de donde, $$\begin{array}1 \sin{\phi}=-\sin{\omega} & \cos{\phi}=\cos{\omega}\\ \tan{\phi}=-\tan{\omega}&~~ \cot{\phi}=-\cot{\omega}\\ \sec{\phi}=\sec{\omega}~~~~&~~ \csc{\phi}=-\csc{\omega} \end{array}$$
Para más contenidos y luego clic en la pestaña del contenido deseado.
Convertir a radianes los ángulos siguientes: $$\textcolor{#ff0080}{1}.~~\ 270°~~~~~~~~\textcolor{#ff0080}{2}.~~480°$$
Convertir a grados los ángulos siguientes: $$\textcolor{#ff0080}{1}.~~\frac{\pi}{3}~{\rm {\rm rad}}$$ $$\textcolor{#ff0080}{2}.~~\frac{\pi}{6}~{\rm rad}$$
Ángulos complementarios. La medida de un ángulo es el duplo de la medida de su complemento disminuido en seis grados. Determinar la medida de los ángulos.
Ángulos suplementarios. Determine la medida de dos ángulos suplementarios si la medida de uno de ellos es el triplo del otro disminuido en cinco grados.
Determinar todas las funciones trigonométricas del ángulo agudo \(\theta\), si sabe que \(\cot{\theta}=3/2\)
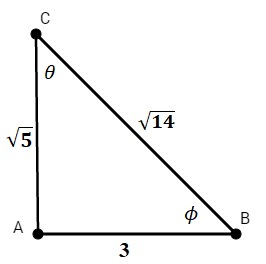Dada la figura de la izquierda determinar las funciones de los ángulos agudos phi \(\phi\) y theta \(\theta\).
Ángulos complementarios. Determinar las funciones trigonométricas de dos ángulos complementarios, \(\phi\) y \(\theta\) si se sabe que \(\sec{\phi}=9/4\)
Funciones de un ángulo en el plano. Determinar todas las funciones trigonométricas del ángulo theta, dadas las condiciones siguientes.
\begin{align}
&1.~~\cot{\theta=\frac{3}{2}}~~ \mathrm{donde}~~180°\leq \theta \leq 270°\\
&2.~~\csc{\theta}=-\frac{5}{7}~~ \mathrm{donde}~~270°\leq \theta \leq 360°\\
&3.~~\sec{\theta}=-{\frac{5}{4}} ~~\mathrm{donde}~~90°\leq \theta \leq 180°\end{align}