Errores de medidas.

En muchos casos cuando se realizan mediciones es imposible determinar la medición sin cometer algún tipo de error, estos se deben a distintas causas que pueden ser tanto humanos, ambientales o del instrumento que su usa para la medición. Los errores por lo general se clasifican en tres categorías principales, burdos, sistemáticos y accidentales.

   Errores burdos.
Se dice que un error es burdo o de negligencia cuando es de origen humano, ya sea por desconocimiento o por uso de instrumentos inapropiados para la toma de medidas, realizar cálculos erróneos, interpretaciones erróneas de mediciones, entre otros. Estos errores pueden minimizarse teniendo cuidado en los detalles en el quehacer científico.

   Errores sistemáticos.
Se dice que un error es sistemático cuando no es de origen humano, estos pueden ser:
1. Debido a fallas instrumentales producidas por desgaste o partes defectuosas del instrumento de medición.
2. Debido a factores ambientales en los instrumentos de medición.
Las fallas en los instrumentos se pueden minimizar o detectar mediante la revisión y calibración constante del instrumento. En cuanto a los errores ambientales se producen a causa de los efectos del medio ambiente como luz, temperatura, campo magnético y/o electrostático, humedad, presión, entre otros. Estos se pueden minimizar mediante ambientes controlados en laboratorios y/o la espera cuidadosa de las condiciones requeridas para el experimento, si se desea medir la rapidez promedio del viento en una ciudad en cierta época del año y se hace en medio de un huracán sin lugar a duda las mediciones se verán afectada por el fenómeno.

   Errores accidentales o aleatorios.
Se dice que estos tipos de errores son errores provenientes de causas desconocidas. Aun cuando se diseñan experimentos donde las variables están contraladas en algunos casos suele existir errores. Aunque suelen ser los menos, tienen gran importancia en trabajos de gran exactitud y la manera de intentar contrarrestarlos es repitiendo el experimento una y otra vez para lograr una mejor aproximación de lo medido y recurrir al análisis estadístico de mediciones.

   Análisis estadístico de errores.
El análisis estadístico de datos de mediciones consiste en la aplicación de ciertos conceptos estadísticos a los resultados obtenidos en física experimental para la determinación de la analítica del error de la medida también llamado incertidumbre. Para esto se recurre en cuanto sea posible a aumentar en una cantidad considerable el número de mediciones del fenómeno estudiado.

   Valor promedio.
El valor promedio (media aritmética) de un conjunto de datos es igual a la suma de ellos entre el número de datos. Así si \(x_1,\ x_2,\ x_3,\ \ldots,\ x_n\) son las distintas medidas hechas a un fenómeno, donde \(n\) es el número total de mediciones o datos, entonces el valor promedio \(\bar{x}\) está dado por, $$\bar{x}=\sum_{i=1}^{n}\frac{x_i}{n}=\frac{x_1+\ x_2+\ x_3+\ldots+\ x_n}{n}$$

   Error absoluto de una medición.
Al organizar las distintas mediciones de un seceso estas pueden organizarse teniendo como centro su media aritmética, así la desviación de una medida mide que tan cerca (o lejos) está una medida con respecto del valor promedio de la medición.

Sean \(\bar{x}\) y \(x_i\) el valor promedio y una de las mediciones respectivamente, entonces la desviación de la medida \(x_i\) denotada por \(E_i\) (en este texto) se define como el valor absoluto de la diferencia de \(x_i-\bar{x}\), esto es,$$ E_i=\left|x_i-\bar{x}\right|$$ y es conocido como el error absoluto de la medida \(x_i\).

   Error absoluto promedio.
Es la desviación media de las mediciones (promedio de los errores absolutos). Mide el margen de error (limites dentro de los cuales está la medida) y tiene unidades iguales que la medidas.
Si \(E_1,E_2, \ldots, E_n\) son los errores absolutos de las n mediciones hechas, entonces el error absoluto promedio denotado por \(E_m\) (en los texto de estadística se denota por \(D_m\) se define como: $$E_m=\sum_{i=1}^{n}\frac{E_i}{n}=\frac{E_1+E_2+\ldots E_3}{n}$$

   Forma científica de una medida.
Ya se ha visto que medir es comparar una cantidad con su unidad de medida para determinar cuántas veces el patrón de medida cabe en una cantidad. Así para expresar la medida \(x_i\) junto a su imprecisión o margen de error cometido, se escribe, $$x_i= x_m \pm E_m$$ La cual es conocida como la forma científica de la medida \(x_i\) y expresa que la medida \(x\) se encuentra dentro del intervalo \(x_m-E_m\le x\le x_m+E_i\)

Para más contenidos clic en Ir arriba y luego clic en la pestaña del contenido deseado.

Vectores y determinantes.

El término vector es empleado en ciencia y matemática para denotar una cantidad la cual tiene magnitud (tamaño) y dirección. Algunas cantidades físicas como el desplazamiento, las velocidades, las fuerzas, ente otras son de naturaleza vectoriales (necesitan para quedar bien especificada que se exprese su tamaño y dirección). Si se pide que una persona realice una fuerza para mover un mueble ¿Hacia dónde debe la persona dirigir su esfuerzo físico? Piense en que se quería mover el mueble hacia la derecha y la persona dirigió su fuerza hacia la izquierda. ¿Se obtendrá el resultado esperado?

Un vector es un ente matemático que tiene módulo (magnitud) y dirección, descripto geométricamente con una semirecta o rayo (flecha de un solo sentido). El módulo representa “el cuánto” que tan grande o pequeño es el vector, la dirección es el menor ángulo medido al eje \(x\) positivo en sentido contrario a las agujas del reloj (si es en el plano) y si es en el espacio a través de los ángulos que forma el vector con los vectores canónicos (se estudian más adelante).

Representación de vectores.
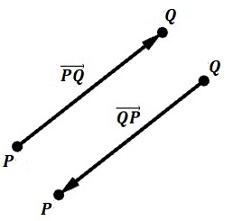La primera representación de vectores es como un segmento de recta dirigido desde un punto \(P\) hasta un punto \(Q.\) donde \(P\) es el punto inicial (cola) y \(Q\) es el punto final (punta). Así en la figura de la izquierda el vector \( \vec{PQ}\neq\vec{QP}\) ya que tienen igual dirección (ángulo medido al eje \(x\) positivo), pero sentido opuesto.

Componentes de un vector.
Es posible representar un vector de distintas formas las más comunes y de uso en ciencias físicas son:
Por una letra en negritas o por una letra con una flecha en dirección izquierda a derecha sobre ella, por ejemplo, \( \mathbf{u}=\left< u_1,u_2,u_3\right>\) un en forma de una matriz renglón (o columna si se desea) donde las cantidades \(u_1,u_2,u_3\cdots u_n\) son llamadas componentes del vector.

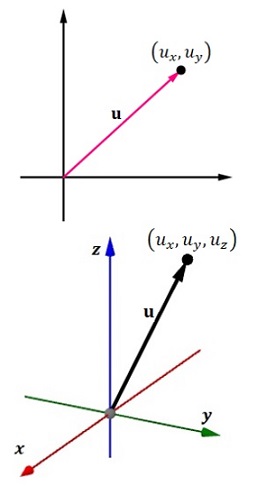
En cuanto a la representación gráfica un vector puede ser en elemento del plano o del espacio. En el caso de que el vector pertenezca al espacio de coordenadas por convención se utilizará el sistema de coordenadas espaciales dextrógiro (sistema derecho) como se muestra en la ###.

Sea el punto \(P\left(p_1,p_2\right)\) y sea el punto \(Q\left(q_1,q_2\right)\) en el plano o \(P\left(p_1,p_2,p_3\right)\) y \(Q\left(q_1,q_2,q_3\right)\) si es en el espacio, las coordenadas del vector \(\mathbf{u}\) que va desde \(P\) hacia \(Q\) se representa en función de sus componentes como,

Componentes de un vector \(\mathbf{u}\)

\(\mathbf{u}=\left< q_1-p_1,q_2-p_2\right>=\left< u_x,u_y\right>\) para el plano.
\(\mathbf{u}=\left< q_1-p_1,q_2-p_2,q_3-p_3\right>=\left< u_x,u_y,u_z\right>\).

Vector de posición.
Si las coordenadas del punto de inicio de un vector son \(Q\left(0,0,0\right)\) entonces el vector \(\mathbf{r}\) que va desde \(Q\) hasta el punto \(P\left(p_x,p_y,p_z\right)\) queda definido por las coordenadas de \(P\left(p_x,p_y,p_z\right)\) y es llamado vector de posición por unir el origen de coordenadas con el punto, esto es \(\mathbf{r}=\left< p_x,p_y,p_z\right>\)

Módulo o magnitud de un vector.
Sea \(\mathbf{u}=\left< u_x,u_y,u_z\right>\) un vector en el espacio (si es en el plano \(u_z=0\)) entonces el módulo o longitud del vector también llamado longitud o norma por algunos autores se define como la raíz cuadrada de la suma de los cuadrados de sus componentes, esto es

Módulo de un vector

\begin{align} ||\mathbf{u}||&=\sqrt{u_x^2+u_y^2}~~~~~~ {\rm para ~el~ plano.}\\ ||\mathbf{u}||&=\sqrt{u_x^2+u_y^2+u_z^2}~~~~ {\rm para~ el ~espacio.} \end{align} Ejemplo. Dados los puntos los puntos \(P\left(2,\ 3,\ 5\right)\) y \(Q(8,6,10)\) determinar los vectores \(\mathbf{u}\) y \(\mathbf{u}\) que van desde P a Q y desde Q hasta P respectivamente al junto de sus módulos de cada vector.
Solución: aplicando la definición para componentes de un vector, \begin{align} \mathbf{u}&=\left< q_1-p_1,q_2-p_2,q_3-p_3\right>=\left< 6,3,5\right>\\ \mathbf{v}&=\left< p_1-q_1,p_2-q_2,p_3-q_3\right>=\left< -6,-3,-5\right> \end{align} de donde se observa que las componentes del vector \(\mathbf{u}\) son los inversas a las componentes del vector \(\mathbf{v}.\) Para el módulo de los vectores se aplica, \begin{align} ||\mathbf{u}||&=\sqrt{u_x^2+u_y^2+u_z^2}\\ ||\mathbf{u}||&=\sqrt{6^2+3^2+5^2}\\ ||\mathbf{u}||&=\left|\left|\vec{QP}\right|\right|=\sqrt{70} \end{align} Que los módulos de los vectores sean iguales, ocurre debido a que los vectores representan el mismo segmento de recta con dirección contraria.

Vector nulo o cero.
Se denomina vector cero o vector nulo al vector en el cual todas las componentes son cero y por tal razón su módulo es cero. Si el módulo de un vector es cero, entonces obligatoriamente \( \mathbf{u}=\mathbf{0}\)

Vectores unitarios.
Se dice que un vector unitario \(\mathbf{u}\) denotado por \(\hat{\mathbf{u}}\) es un vector tal que \(\mathbf{u}\) es uno, esto es \(||\hat{\mathbf{u}}||=1.\) Un vector \(\hat{\mathbf{u}}\) en la dirección de otro vector cualquiera \(\mathbf{v}\) queda determinado al dividir las componentes del vector \(\mathbf{v}\) entre su módulo.

Vector unitario \(\hat{\mathbf{u}}\) en dirección \( \mathbf{v}\)

$$\hat{\mathbf{u}}=\frac{\mathbf{v}}{||\mathbf{v}||}=\frac{\mathbf{1}}{||\mathbf{v}||}\mathbf{v}$$ Ejemplo. Determinar el vector unitario en la dirección del vector \(\mathbf{v}=\left< 3,0,4\right>\)
Solución: aplicando la definición de vector unitario, \begin{align} \hat{\mathbf{u}}&=\frac{\mathbf{1}} {\left|\left|\mathbf{v}\right|\right|}\mathbf{v}\\ \hat{\mathbf{u}}&=\frac{1}{\sqrt{3^2+0^2+4^2}}\left< 3,0,4\right>\\ \hat{\mathbf{u}}&=\left<\frac35,0,\frac45\right> \end{align} Vectores unitarios canónicos
En términos de las coordenadas espaciales \(x,\ y,z,\) se definen los llamados vectores unitarios canónicos, como:
Para el plano \( \mathbf{i}=\left< 1,0\right>;~ \mathbf{j}=\left< 0,1\right>\)
Para el espacio \(\mathbf{i}=\left< 1,0,0\right>;~ \mathbf{j}=\left< 0,1,0\right>, ~\mathbf{k}=\left< 0,0,1\right>\)
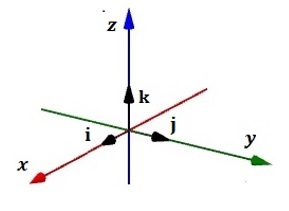La descripción geométrica de los vectores canónicos se muestra en la figura de la izquierda.

En función de estos vectores un vector \(\mathbf{v}\) se escribe como, $$\mathbf{v}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k}$$ donde \(v_x, v_y\) y \(v_z\) son las componentes del vector.

Si se conoce la dirección \(\phi\) de un vector en el plano \(\mathbf{v},\) entonces un vector unitario en la dirección del vector \(\mathbf{v}\) es el vector $$\hat{\mathbf{u}}=\cos{\phi}\mathbf{i}+\sin{\phi}\mathbf{j}.$$

Operaciones con vectores.

Múltiplo escalar de un vector.
En el contexto de los vectores los números son llamados escalares, así cualquier \(c|c\in\mathbb{C}\) es un escalar, el producto de un escalar \(c\) por un vector \(\mathbf{u}\) esta dado por \(c\mathbf{u}=\left< cu_x,cu_y,cu_z\right>.\)

Si el módulo de un vector \(\mathbf{u}\) se multiplica por un escalar \(c\) (distinto de cero por convención) el resultado es un nuevo vector cuyo modulo es c veces el módulo del vector \(\mathbf{u},\) esto es, y de esto se concluye que,

Módulo de un múltiplo escalar.

$$||c\mathbf{u}||=c||\mathbf{u}||$$ La demostración a esto es bastante simple, partiendo de \(c\mathbf{u}=(cu_x,cu_y,cu_z):\) \begin{align} \left|\left|c\mathbf{u}\right|\right|&=\sqrt{\left(cu_x\right)^2+\left(cu_y\right)^2+\left(cu_z\right)^2}\\ \left|\left|c\mathbf{u}\right|\right|&=\sqrt{c^2u_x^2+c^2u_y^2+c^2u_z^2}\\ \left|\left|c\mathbf{u}\right|\right|&=\sqrt{c^2\left(u_x^2+u_y^2+u_z^2\right)}\\ \left|\left|c\mathbf{u}\right|\right|&=c\sqrt{\left(u_x^2+u_y^2+u_z^2\right)}\\ \left|\left|c\mathbf{u}\right|\right|&=c\left|\left|\mathbf{u}\right|\right| l.q.q.d.\end{align}

Adición de vectores.
La adición de los vectores \(\mathbf{u}\) y \(\mathbf{v}\) en el plano puede realizarse gráficamente por un método conocido como el método del paralelogramo el cual consiste en la representación gráfica de los vectores de modo que el punto inicial de \(\mathbf{v}\) coincide con el punto final de \(\mathbf{u}\) y el vector resultante \(\mathbf{r}=\mathbf{u}+\mathbf{v}\) es el vector cuyo punto inicial coincide con el punto inicial de \(\mathbf{u},\) y cuyo final coincide con el punto final de \(\mathbf{v}.\) Aunque este método es funcional por considerarse un método tedioso se prefiere hacer énfasis en la adición de vectores a través del método de las componentes. El método del paralelogramo (también llamado método del triángulo) se puede observar en las figuras de la izquierda.

Adición de vectores por componentes.
Sean los vectores \(\mathbf{u}\) y \(\mathbf{v}\) definidos en el plano o el espacio, entonces el vector resultante \(\mathbf{r}=\mathbf{u}+\mathbf{v}\) está dado por,

Suma vectorial por componentes \(\mathbf{r}=\mathbf{u}+\mathbf{v}\)

\(\mathbf{r}=(u_x+v_x)\mathbf{i}+(u_y+v_y)\mathbf{j}\) para el plano.
\(\mathbf{r}=(u_x+v_x)\mathbf{i}+(u_y+v_y)\mathbf{j}+(u_z+v_z)\mathbf{k}\) para el espacio.

Ejemplo. Dados \(\mathbf{u}=\left< 3,4\right>\) y \(\mathbf{v}=\left< -2,-1\right>\) determinar \(\mathbf{r}=\mathbf{u}+\mathbf{3v}.\)
Solución:\(\mathbf{r}=\left< 3+3(-2),4+3(-1)\right>=\left<-3,1\right>\)

Ejemplo. Dado el vector \(\mathbf{u}=3\mathbf{i}+4\mathbf{j}-5\mathbf{k}\) y el vector \(\mathbf{v}=4\mathbf{i}-2\mathbf{k}\) determinar \(\mathbf{r}=\mathbf{2u}+\mathbf{5v}.\)
Solución: aplicando la definición del producto de un escalar y un vector \(c\mathbf{u}=\left< cu_x,cu_y,cu_z\right>\) al junto con la definición de suma, \begin{align} \mathbf{r}&=(u_x+v_x)\mathbf{i}+(u_y+v_y)\mathbf{j}+(u_z+v_z)\mathbf{k}\\ \mathbf{r}&=2(3\mathbf{i}+4\mathbf{j}-5\mathbf{k})+5(4\mathbf{i}-2\mathbf{k})\\ \mathbf{r}&=6\mathbf{i}+8\mathbf{j}-10\mathbf{k}+\mathbf{20i}-10\mathbf{k}\\ \mathbf{r}&=\mathbf{2}6\mathbf{i}+8\mathbf{j}-20\mathbf{k}\end{align}

Producto escalar de dos vectores.

Dados dos vectores \(\mathbf{u}=\left< u_1,u_2,u_3,⋯,u_n\right>\) y \(\mathbf{v}=\left< v_1,v_2,v_3,⋯,v_n\right>\) entonces el producto escalar o producto interno de ellos, también llamado producto punto por su notación \(\mathbf{u}\cdot\mathbf{v}\) se define como,

Producto escalar de vectores

$$\mathbf{u}\cdot\mathbf{v}=u_1v_1+u_2v_2++u_3v_3+\cdots+u_nv_n$$ Ejemplo. Determinar el producto escalar de los vectores dados. \begin{align} a.\ \mathbf{u}&=\left< 7,11\right> ~{\rm y} ~\mathbf{v}=\left< 3,9\right>\\ b.\ \mathbf{u}&=\left< 5,7,11\right>~ {\rm y}~ \mathbf{v}=\left< -2,0,-3\right> \end{align} Solución: aplicando la definición de producto punto. \begin{align} a.&~~\mathbf{u}\cdot\mathbf{v}=7(3)+11\left(9\right)=120\\ b.&~~\mathbf{u}\cdot\mathbf{v}=5\left(-2\right)+7\left(0\right)+11\left(-3\right)=-43 \end{align} Propiedades del producto escalar.
El producto escalar hereda algunas de las propiedades directas de la multiplicación como se muestra a continuación.
1. Múltiplo escalar: \(c(\mathbf{u}\cdot\mathbf{v})=c\mathbf{u}\cdot\mathbf{v}=\mathbf{u}\cdot c\mathbf{v}\)
2. Conmutativa: \(\mathbf{u}\cdot\mathbf{v}=\mathbf{v}\cdot\mathbf{u}\)
3. Distributiva: \(\mathbf{r}\cdot(\mathbf{u}+\mathbf{v})=\mathbf{r}\cdot\mathbf{u}+\mathbf{r}\cdot\mathbf{v}\)
4. Elemento absorbente: \(\mathbf{0}\cdot\mathbf{u}=\mathbf{0} \)
5. Producto escalar consigo mismo: \(\mathbf{u}\cdot\mathbf{u}=||u||^2\)

Ángulo entre dos vectores.
Existen diversas formas de observar el ángulo entre dos vectores, una de ella es a través de la definición alternativa del producto escalar. Sean los vectores \(\mathbf{u}\) y \(\mathbf{v}\) dos vectores cualquiera no nulos, definidos en el plano o en el espacio y sea \(\theta\) el ángulo entre ellos, entonces,

Ángulo entre dos vectores

$$\cos{\theta}=\frac{\mathbf{u}\cdot\mathbf{v}}{||u||||v||} ⟹ \theta=\cos^{-1}\frac{\mathbf{u}\cdot\mathbf{v}}{||u||||v||}$$ La demostración a esto se obtiene de manera directa de la ley de los cosenos, y las propiedades del producto escalar.

Ejemplo. Determinar el ángulo entre los vectores dados para cada una de las situaciones. \begin{align} 1.~&\mathbf{u}=\left< 2,3,5\right> ~{\rm y}~ \mathbf{v}=\left< 3,4,7\right>\\ 2.~&\mathbf{u}=\left< 2,3,0\right> ~{\rm y}~ \mathbf{v}=\left< 7,5,0\right>\\ 3.~&\mathbf{i}=\left< 1,0,0\right> ~{\rm y}~ \mathbf{k}=\left< 0,0,1\right>\\ \end{align} Solución: aplicando la definición del ángulo, \begin{align} \theta=&\cos^{-1}\frac{\mathbf{u}\cdot\mathbf{v}}{||u||||v||}\\ \theta_1=&\cos^{-1}{\frac{2\left(3\right)+3\left(4\right)+5\left(5\right)}{\sqrt{2^2+3^2+5^2}\sqrt{3^2+4^2+7^2}}}=\cos^{-1}{\left(\frac{43}{2\sqrt{703}}\right)}\approx35.8°\\ \theta_2=&\cos^{-1}{\frac{2\left(7\right)+3\left(5\right)+0\left(0\right)}{\sqrt{2^2+3^2+0^2}\sqrt{7^2+5^2+0^2}}}=\cos^{-1}{\left(\frac{29}{\sqrt{962}}\right)}\approx20.8°\\ \theta_3=&\cos^{-1}{\frac{1\left(0\right)+0\left(0\right)+0\left(1\right)}{\sqrt{1^2+0^2+0^2}\sqrt{0^2+0^2+1^2}}}=\cos^{-1}{\left(\frac{0}{1}\right)}=0°\\ \end{align} Note de este resultado que el producto escalar \(\mathbf{i}\cdot\mathbf{k}=0,\) esto no es casualidad por ser los vectores canónicos ortogonales.

Definición de vectores ortogonales

El vector \(\mathbf{u}\) es ortogonal a \(\mathbf{v}\) si y solo si \(\mathbf{u}\cdot\mathbf{v}=0\)

Productos vectoriales.

Como una primera aplicación de los determinantes se presenta el producto vectorial de dos vectores \(\mathbf{u}\) y \(\mathbf{v}\) denotado como \(\mathbf{u}\times\mathbf{v}\) también llamado producto cruz, el cual es de gran aplicación en ciencias físicas, este puede definirse en términos del determinante como sigue:

Definición de producto vectorial.

Sean los vectores \( \mathbf{u}=u_1\mathbf{i}+u_2\mathbf{j}+u_3\mathbf{k}~~{\rm y}~~ \mathbf{v}=v_1\mathbf{i}+v_2\mathbf{j}+v_3\mathbf{k}\) tales que \(\phi\) es el ángulo entre ellos, entonces el vector \( \mathbf{r}=\mathbf{u}\times\mathbf{v}\) es un vector tal que \(||\mathbf{r}||=||\mathbf{u}||||\mathbf{v}||\sin{\phi}\) el cual es ortogonal tanto a \(\mathbf{u}\) como a \(\mathbf{v}\) que escrito en términos de su componentes es, $$\mathbf{u}\times\mathbf{v}=(u_2v_3-u_3v_2)\mathbf{i}+(u_1v_3-u_3v_1)\mathbf{j}+(u_1v_2-u_2v_1)\mathbf{k}$$ Al aplicar esta definición a los vectores canónicos \(\mathbf{i},\mathbf{j},\ \mathbf{k}\) se obtiene; \begin{array}{l} \mathbf{i}\times\mathbf{j}=\mathbf{k}& \mathbf{j}\times\mathbf{k}=\mathbf{i}& \mathbf{k}\times\mathbf{i}=\mathbf{j}\\ \mathbf{i}\times\mathbf{k}=-\mathbf{j}& \mathbf{k}\times\mathbf{j}=-\mathbf{i}& \mathbf{j}\times\mathbf{i}=-\mathbf{k} \end{array} Se pueden recordar estos resultados al considerar el producto vectorial de los vectores canónicos en un círculo el cual puede ser recorrido en sentido antihorario u horario. Cuando se recorre el círculo en sentido antihorario se obtienen los primeros tres resultados. Cuando es en sentido horario los demás.

En la práctica es más simple recordar la definición de producto vectorial al considerar su forma alternativa como un determinante.

Definición alternativa del producto vectorial.

Sean los vectores \(\mathbf{u}=\left< u_1,u_2,u_3\right>\) y \( \mathbf{v}=\left< v_1,v_2,v_3\right>\) que también pueden escribirse en función de los vectores unitarios \(\mathbf{i},\mathbf{j},\mathbf{k},\) como, \begin{align} \mathbf{u}=&u_1\mathbf{i}+u_2\mathbf{j}+u_3\mathbf{k}\\ \mathbf{v}=&v_1\mathbf{i}+v_2\mathbf{j}+v_3\mathbf{k} \end{align} entonces el producto vectorial \(\mathbf{u}\times\mathbf{v}\) es, $$\mathbf{u}\times\mathbf{v}=\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\u_1&u_2&u_3\\v_1&v_2&v_3\\\end{matrix}\right|=\left|\begin{matrix}u_2&u_3\\v_2&v_3\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}u_1&u_3\\v_1&v_3\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}u_1&u_2\\v_1&v_2\\\end{matrix}\right|\mathbf{k}$$

Se debe notar que en sentido estricto esta expresión no es un determinante, ya que los elementos del primer renglón (fila) son vectores y no números, sin embargo, obviando este detalle es muyo más fácil realizar el producto cruz de dos vectores. Otro elemento importante es recordar que a diferencia del producto escalar el producto cruz es un vector no un número.

Se tienen muchas aplicaciones del producto vectorial tanto en matemática como en ciencias físicas. Algunas cantidades físicas de naturaleza vectorial se explican analíticamente por medio de este producto y en el campo de las matemáticas se pueden describir áreas y volúmenes de manera simple, este hecho se ilustra a continuación en los ejemplos siguientes.

Ejemplo. Momento de torsión. el momento de torsión \(\vec{\mathbf{\tau}}\) (tau) también llamado vector torca, par de torsión o momento de fuerza es un vector el cual “describe” el movimiento de un cuerpo que girar sobre un eje fijo, y mediante la expresión, $$\vec{\mathbf{\tau}}=\vec{\mathbf{r}}\times\vec{\mathbf{F}}.$$ Se aplica una fuerza \(\vec{\mathbf{F}}=\left(3.0\hat{\mathbf{i}}+5.0\hat{\mathbf{j}}\right)N\) sobre un objeto el cual puede girar en torno a un eje fijo en la dirección del eje \(z.\) Si la fuerza se aplica en un punto cuya ubicación es, \( \vec{\mathbf{r}}\left(7.0\hat{\mathbf{i}}+7.0\hat{\mathbf{j}}\right)m\) determinar la magnitud del vector momento de torsión.
Solución: la magnitud del vector torca es \(||\vec{\mathbf{\tau}}||=\sqrt{\tau_x^2+\tau_y^2+\tau_z^2}.\) Para hallar las componentes se realiza el producto cruz. \begin{align} \mathbf{\tau}=&\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\7.0&7.0&0.0\\3.0&5.0&0.0\\\end{matrix}\right|=\left|\begin{matrix}7.0&0.0\\5.0&0.0\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}7.0&0.0\\3.0&5.0\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}7.0&7.0\\3.0&5.0\\\end{matrix}\right|\mathbf{k}\\ \mathbf{\tau}=&\left(35-21\right)\mathbf{k}=14\mathbf{k}Nm\\ \left|\left|\mathbf{\tau}\right|\right|=&\sqrt{\left(14Nm\right)^2}=14Nm \end{align} Ejemplo. Fuerza magnética. La fuerza magnética (medida en tesla T) a la cual es sometida un cuerpo está dada por $$\vec{\mathbf{F}}=q\mathbf{v}\times\mathbf{B}$$ donde \(q\) es la carga, \(\vec{\mathbf{v}}\) es el vector velocidad y \(\mathbf{B}\) es el vector de campo magnético. Un protón se mueve con una velocidad \(\mathbf{v}=(3\mathbf{i}\ – 4j + 2k) m/s\) en una región donde el campo magnético es \(\mathbf{B}=(5\mathbf{i}\ +\ 2\mathbf{j}\ – 3k) T.\) ¿Cuál es la magnitud de la fuerza magnética que experimenta esta carga?
Solución: la magnitud de la fuerza está dada por \( ||\vec{\mathbf{F}}||=qv×B\) donde \(q=1.60\times{10}^{-19}C\) es la carga del protón. \begin{align} \mathbf{v}\times\mathbf{B}=&\left|\begin{matrix}\mathbf{i}&\ \ \ \ \mathbf{j}&\ \ \ \mathbf{k}\\3&-4&\ \ \ 2\\5&\ \ \ 2&-3\\\end{matrix}\right|=\left|\begin{matrix}-4&\ \ 2\\2&-3\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}3&\ \ 2\\5&-3\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}3&-4\\5&\ \ \ \ 2\\\end{matrix}\right|\mathbf{k}\\ \mathbf{v}\times\mathbf{B}=&(8\mathbf{i}+19\mathbf{j}+26\mathbf{k})T m/s\\ ||\mathbf{v}\times\mathbf{B}||=&\sqrt{8^2+19^2+26^2}=\sqrt{1101}Tms\\ F=&qv×B=1.60×10^{-19}C \sqrt{1101}Tms\\ F=&5.31\times{10}^{-18}N \end{align} Ejemplo. Área de un paralelogramo. El área de un paralelogramo en unidades cuadradas \((u^2),\) cuyos lados adyacentes son los vectores \(\mathbf{u}\) y \(\mathbf{v}\) está dada por $$A=||\mathbf{u}\times\mathbf{v}||$$ Determinar el área del paralelogramo de lados adyacentes \(\mathbf{u}=(2\mathbf{i}\ +\ 2\mathbf{j}\ – 4k)\) y \(\mathbf{v}=(-2\mathbf{i}\ +3\mathbf{j}\ +\ 4\mathbf{k})\) \begin{align} \mathbf{u}\times\mathbf{v}=&\left|\begin{matrix}\ \ \ \mathbf{i}&\mathbf{j}&\ \ \ \mathbf{k}\\\ \ \ 2&2&-4\\-2&3&\ \ \ 4\\\end{matrix}\right|=\left|\begin{matrix}2&-4\\3&\ \ \ 4\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}\ \ \ 2&-4\\-2&\ \ \ 4\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}\ \ \ 2&2\\-2&3\\\end{matrix}\right|\mathbf{k}\\ \mathbf{u}\times\mathbf{v}=&20\mathbf{i}+10\mathbf{k}\\ A=&\left|\left|\mathbf{u}\times\mathbf{v}\right|\right|\\ A=&\sqrt{{20}^2+{10}^2}=\sqrt{500}u^2 \end{align} Como puede notar existen diversas aplicaciones para un determinante de orden \(3\times3\) estos son solo algunos de los múltiples ejemplos que puede encontrar al estudiar física o matemáticas. Aun queda mucho por conocer.

Para más contenidos clic en Ir arriba y luego clic en la pestaña del contenido deseado.