Definición analítica de determinante.

Expansión de Laplace.
Dada una matriz cuadra \(A\) de orden \(n\times n\) el determinante de está denotado por \({\rm det}(A)\) o \(|A|\) es la suma de los productos de los elementos de alguna de su filas (o columnas) y sus respectivos cofactores, esto es \(\sum{a_{ij}C_{ij}}.\) Así por ejemplo si se toma la primera fila de la matriz \(A\) entonces, $$\left|A\right|=a_{11}C_{11}+a_{12}C_{12}+a_{13}C_{13}+\cdots+a_{1n}C_{1n}$$ Esta suma que se escribe de manera abreviada como \(\sum{a_{ij}C_{ij}}\) es llamada expansión de Laplace en honor al matemático Pierre-Simon Laplace a quien se le atribuye haber dado con la expresión. A continuación, se presenta el cálculo de determinantes usando este método.

Ejemplo. Determinante de una matriz \(\mathbf{2}\times\mathbf{2}.\) Deducir una expresión para el determinante de una matriz \(2\times2\) dada la matriz, $$A=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right)$$ Solución: aplicando la expansión de Laplace para la primera fila, \begin{align} &\left|A\right|=a_{11}C_{11}+a_{12}C_{12}\\ &\left|A\right|=a_{11}\left(-1\right)^{1+1}\left|a_{21}\right|+a_{12}\left(-1\right)^{1+2}|a_{22}|\\ &\left|A\right|=a_{11}a_{21}-a_{12}a_{22}\end{align} De donde se concluye que el determinante de una matriz \(2\times2\) es igual al producto de los elementos de su diagonal principal, menos el producto de los elementos de su diagonal secundaria.

Ejemplo. Un determinante \(\mathbf{2}\times\mathbf{2}.\) Calcular \({\rm det}(A)\) para, $$A=\left(\begin{matrix}2&3\\5&7\\\end{matrix}\right)$$ Solución: por el resultado del ejemplo anterior \({\rm det}(A)=2(7)-3(5)=-1\)

Ejemplo. Un determinante trigonométrico. Calcular \({\rm det}(A)\) si $$A=\left(\begin{matrix}\sin{u}&-\cos{u}\\\cos{u}&\sin{u}\\\end{matrix}\right)$$ Solución: \({\rm det}(A)=\sin^2{x}+\cos^2{x}=1.\)

Ejemplo. Jacobiano de coordenadas polares. Un factor de cambio de variable de un sistema coordenado a otro muy importante en el estudio del cálculo multi variables es conocido con el nombre de jacobiano, este es el valor absoluto de un determinante de derivadas parciales, a continuación, se presenta el jacobiano en el cambio a coordenadas polares, la cual transforma un punto \(P\left(x,y\right)\) en otro punto \(P\left(r,\phi\right)\) \begin{align} J\left(r,\phi\right)&=\left|\begin{matrix}\cos{\phi}&-r \sin\phi\\\sin{\phi}&r\cos{\phi}\\\end{matrix}\right|\\ J\left(r,\phi\right)&=r\left(\cos{\phi}\right)^2+r\left(\sin{\phi}\right)^2\\ J\left(r,\phi\right)&=r\left(\left(\cos{\phi}\right)^2+\left(\sin{\phi}\right)^2\right)\\ J\left(r,\phi\right)&=r\end{align}

Ejemplo. Determinante de una matriz \(3\times3.\) Usar la expansión de Laplace para calcular el determinante de la matriz, $$A=\left(\begin{matrix}1&2&5\\3&1&3\\2&4&0\\\end{matrix}\right)$$ Solución: aplicando la expansión de Laplace para la primera fila, \begin{align} &{\rm det}(A)= a_{11}C_{11}+a_{12}C_{12}+a_{13}C_{13}\\ &{\rm det}(A)= 1\left(-1\right)^{1+1}\left|\begin{matrix}1&3\\4&0\\ \end{matrix}\right|+2\left(-1\right)^{1+2}\left|\begin{matrix}3&3\\2&0\\\end{matrix}\right|+5\left(-1\right)^{1+3}\left|\begin{matrix}3&1\\2&4\\\end{matrix}\right|\\ &{\rm det}(A)=1\left(1\left(0\right)-3\left(4\right)\right)-2\left(3\left(0\right)-3\left(2\right)\right)+5\left(3\left(4\right)-1\left(2\right)\right)\\ &{\rm det}(A)=1(-12)-2(-6)+5(10)\\ &{\rm det}(A)=-12+12+50=50\end{align}

En la introducción al tema se dijo que al usar la expansión de Laplace \({\rm det}(A)\) o es la suma de los productos de los elementos de alguna de su filas (o columnas) y sus respectivos cofactores, esto quiere decir que no importa la fila o columna que se utilice como pivote, el resultado será el mismo y debido a esto se suele tomar como fila o columna pivote aquella que tenga más ceros o más unos, o en su defecto aquella fila o columna cuyos valores absolutos de los elementos sean más pequeños, este hecho se ilustra en los dos siguientes ejemplos.

Ejemplo. Calcular el valor del determinante de las matrices dadas. $$A=\left(\begin{matrix}1&2&5\\7&0&-3\\-5&0&7\\\end{matrix}\right)\ \ \ \ \ \ \ \ B=\left(\begin{matrix}1&2&3&4\\2&3&7&1\\3&0&0&1\\2&1&5&7\\\end{matrix}\right)$$ Solución: de la definición de expansión de Laplace el determinante de una matriz es la suma de los \( a_{ij}C_{ij}\) (elemento \(a_{ij}\) por cofactor \(C_{ij}).\) Aunque el determinante de \(A\) puede ser calculado por Sarrus, como práctica ambos determinantes se harán por expansión de Laplace.
Para \(det\mathbf{A}\) se observa que la segunda columna tiene dos ceros, por tanto, tomando esta columna como pivote, $${\rm det}(A)=2\left(-1\right)^3\left|\begin{matrix}7&-3\\-5&7\\\end{matrix}\right|+0\left(-1\right)^4\left|\begin{matrix}1&5\\-5&5\\\end{matrix}\right|+0\left(-1\right)^5\left|\begin{matrix}1&5\\7&-3\\\end{matrix}\right|$$ Note que es totalmente innecesario escribir la suma de los últimos dos cofactores, ya que los \(a_{ij}=0,\) así que, \({\rm det}(A)=2\left(-1\right)^3(49-15)=-68\)
Para \({\rm det}(B)\) note que la tercera fila tiene, dos ceros y un uno, lo que hace que sea más idónea para usarla como pivote \({\rm det}(B)=\sum{a_{ij}C_{ij}}\) \begin{align} &{\rm det}(B)=3\left(-1\right)^4\left|\begin{matrix}2&3&4\\3&7&1\\1&5&7\\\end{matrix}\right|+1\left(-1\right)^7\left|\begin{matrix}1&2&3\\2&3&7\\2&1&5\\\end{matrix}\right|\\ \\ &{\rm det}(B)=3\left|\begin{matrix}2&3&4\\3&7&1\\1&5&7\\\end{matrix}\right|-\left|\begin{matrix}1&2&3\\2&3&7\\2&1&5\\\end{matrix}\right|\end{align} Expandiendo ahora los determinantes \(3\times3\) pivoteando en las primeras filas en ambos casos entonces, \begin{align} &{\rm det}(B)= 3\left(2\left|\begin{matrix}7&1\\5&7\\\end{matrix}\right|-3\left|\begin{matrix}3&1\\1&7\\\end{matrix}\right|+4\left|\begin{matrix}3&7\\1&5\\\end{matrix}\right|\right)-\left(1\left|\begin{matrix}3&7\\1&5\\\end{matrix}\right|-2\left|\begin{matrix}2&7\\2&5\\\end{matrix}\right|+3\left|\begin{matrix}2&3\\2&1\\\end{matrix}\right|\right)\\ &{\rm det}(B)=3(2(44)-3(20)+4(8))-(8-2(-4)+3(-4))\\ &{\rm det}(B)=3(88-60+32)-(8+8-12)\\ &{\rm det}(B)=3\left(60\right)-\left(4\right)=176\end{align} Como se puede notar, calcular un determinante de un orden mayor al \(3\times3\) puede ser un proceso laborioso, debido a que el proceso es iterativo, sin embargo, el uso de las propiedades de los determinantes facilita en gran manera el trabajo.

Propiedades de los determinantes.
1. Filas o columnas nulas. Si una matriz \(A\) tiene un fila o columna donde todos los elementos \(a_{ij}\) son ceros, entonces \(|A|=0.\)
2. Filas o columnas idénticas o múltiplos escalares. Si una matriz \(A\) posee dos o más filas (o columnas) iguales, o que sean múltiplos escalares una de otra \(|A|=0.\)
3. Determinante de un producto. Si \(A,B,\ C\ldots\) son matrices del mismo orden, entonces \(|ABC|=|A||B||C|\) y además es invariante respecto al orden de multiplicación.
4. Determinante de la Transpuesta. Sea \(A\) una matriz tal que \(A^T\) es su matriz transpuesta entonces \(|A|=|A^T|.\)
5. Factorizando un múltiplo escalar. Si los elementos de una fila (o columna) de una matriz A poseen un factor común \mu entonces \(|A|\) puede ser calculado como \(|A|=\mu|A^\prime|\) donde \(A^\prime\) es la matriz que resulta luego de extraer el factor común \(\mu.\) Además, si \(\mu\) es un factor tal que \(A\) es múltiplo escalar de \(\mu\) entonces \(|A|=\mu^n|A^\prime|\)
6. Intercambio de filas o columnas. Si se intercambian dos filas (o columnas) de una matriz \(A\) entonces, \(|A|\) cambia de signo.
7. Invarianza ante la adición. El determinante \(|A|\) de una matriz es invariante si se suma un múltiplo constante de una de sus filas (o columnas) a otra fila (o columna).
8. Determinante complejo y hermitiana. Sea \(A\) una matriz tal que \(A^\ast\) es su compleja conjugada, entonces \(|A^\ast|={|A|}^\ast\) y por la propiedad cuatro \(|A|=|A^T|\) entonces como la matriz hermitiana \(A^\dagger\) está dada por \(A^\dagger={(A^T)}^\ast\) se tiene que, \(|A^\dagger|=|\left(A^T\right)^\ast|=|A^\ast|=|{A|}^\ast.\)

Ejemplo. Calculando determinantes. Calcular el determinante de cada una de las matrices dadas, (usar propiedades si es posible). $$A=\left(\begin{matrix}1&3&0\\1&3&5\\2&6&10\\\end{matrix}\right)\ \ \ \ \ \ B=\left(\begin{matrix}0&1&2\\2&0&1\\3&4&0\\\end{matrix}\right)\ \ \ \ \ \ C=\left(\begin{matrix}2&3&12&2\\5&1&4&3\\-3&1&4&2\\-7&2&8&1\\\end{matrix}\right)$$ Solución: los determinantes de las matrices \(A\) y \(B\) pueden ser calculados por expansión de Laplace o regla de Sarrus, sin embargo, note que para la matriz \(A\) la segunda columna es un múltiplo escalar de la primera (la primera multiplicada por tres) por tanto \(|A|=0.\) Para la matriz \(B\) no se debe pensar que por ser los elementos de la diagonal principal todos ceros \(|B|=0.\) Por expansión de Laplace para la tercera columna, \begin{align} \left|B\right|&=\sum{a_{ij}C_{ij}}\\ \left|B\right|&=2\left(\left(-1\right)^{1+3}\left|\begin{matrix}2&0\\3&4\\\end{matrix}\right|\right)+1\left(\left(-1\right)^{2+3}\left|\begin{matrix}0&1\\3&4\\\end{matrix}\right|\right)\\ \left|B\right|&=2\left(8\right)1-\left(-3\right)\\ |B|&=19\end{align} Para la matriz \(C\) por ser una matriz de orden \( 4\times4\) antes de pensar en la expansión de Laplace se debe analizar cada una de sus filas y columnas para ver si existe una fila o columna que sean múltiplo escalar de otra, la tercera columna es múltiplo escalar de la segunda y por tanto, \(|D|=0.\)

Ejemplo. Un determinante de una matriz hermitiana. Calcular el determinante de la matriz conjugada hermitiana para, $$A=\left(\begin{matrix}1&3+2i&0\\i&2&7+2i\\5-2i&7-2i&4\\\end{matrix}\right)$$ Solución: por definición la matriz hermitiana es \(A^\dagger={(A^T)}^\ast\) de donde, \begin{align} A^\ast&=\left(\begin{matrix}1&3-2i&0\\-i&2&7-2i\\5+2i&7+2i&4\\\end{matrix}\right)\\ A^\dagger&=\left(\begin{matrix}1&-i&5+2i\\3-2i&2&7+2i\\0&7-2i&4\\\end{matrix}\right)\\ A^\dagger&=8+\left(3+2i\right)\left(7-2i\right)\left(5+2i\right)-\left(7+2i\right)\left(7-2i\right)i-4i\left(3-2i\right)\\ A^\dagger&=88-54i\end{align} Ejemplo Una matriz triangular. Calcular el determinante de la matriz $$A=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{33}\\\end{matrix}\right)$$ Solución: usando expansión de Laplace para el último reglón. $$\left|A\right|=a_{33}\left(-1\right)^6\left|\begin{matrix}a_{11}&a_{12}\\0&a_{22}\\\end{matrix}\right|=a_{11}a_{22}a_{33}$$ Se puede probar si se desea, que igual resultado se hubiera obtenido si la matriz A fuera triangular inferior en vez de triangular superior y de esto se concluye el siguiente teorema.

Determinante de una matriz triangular
Sea \(A\) una matriz triangular de orden \(n,\) entonces \(|A|\) es el producto de los elementos de la diagonal principal, es decir, $$\left|A\right|=a_{11}a_{22}a_{33}a_{44}\cdots a_{nn}$$ Para el caso de las matrices de orden tres por tres, el teorema ya es válido por el ejemplo resuelto, para los demás casos, se puede recurrir a la inducción matemática mediante la notación de Levi-Civita.

Regla de Sarrus para determinantes \(\mathbf{3}\times\mathbf{3}\).

Un método alternativo para el cálculo de un determinante \(3\times3\) lo constituye el método conocido como regla de Sarrus, desarrollado por el matemático Pierre Frédéric Sarrus en el siglo XIX. Este método es considerado tal vez, la forma más simple para el cálculo del determinante \(3\times3.\) Dicho método fue utilizado sin entrar en detalles para escribir la ecuación de un recta en forma de determinante, y se retoma en esta sección, a continuación, su desarrollo.

Dada la matriz $$\mathbf{A}=\left(\begin{matrix}u_{11}&u_{12}&u_{13}\\u_{21}&u_{22}&u_{23}\\u_{31}&u_{32}&u_{33}\\\end{matrix}\right)$$ añadir las pimeras dos filas para una matriz \(5\times3\) o las primeras dos columnas, para una matriz \(3\times5\) (en este caso), trazando diagonales primarias y secundarias como sigue,

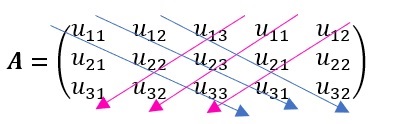
Realizar los productos de los elementos de cada una de las diagonaes, las diagonales primarias (azules) conservan su signo, las secundarías (en rosa) cambian el signo del producto, de donde \({\rm det}A=\)
\(u_{11}u_{22}u_{33}+u_{12}u_{23}u_{31}+u_{13}u_{21}u_{32} -(u_{13}u_{22}u_{31}+u_{11}u_{23}u_{32} +u_{12}u_{21}u_{31})\)

Ejemplo. Una función lineal. En cierta tienda de juguetes el costo de producir tres unidades del juguete tipo A es de $350, mientras que el costo de producir diez unidades es de $700. Suponiendo una relación lineal entre las unidades producidas y el costo, usar determinantes para encontrar la relación y dar una interpretación de su significado.
Solución: sea \(x\) las unidades del juguete tipo A a producir. Como la relación es unidades-costo es lineal tiene la forma \(y=mx+n\) y mediante el uso de determinante está dada por, $$\left|\begin{matrix}x&y&1\\x_1&y_1&1\\x_2&y_2&1\\\end{matrix}\right|=\left|\begin{matrix}x&y&1\\3&350&1\\10&700&1\\\end{matrix}\right|=0$$ Mediante la regla de Sarrus se tiene,

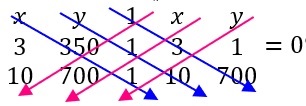
\begin{align} &\textcolor{blue}{350x+10y+2100}-\left(\textcolor{#ff0080}{3500+700x+3y}\right)=0\\ &350x+10y+2100-3500-700x-3y=0\\ &-350x+7y-1400=0\\ &-50x+y-200=0\\ &y=50x+200\end{align} Su interpretación es que el costo variable por unidad es cincuenta peso y el costo fijo es $200.

Ejemplo. Determinante de una matriz \(\mathbf{3}\times\mathbf{3}.\) Usar la regla de Sarrus para calcular el valor del \({\rm det} \ \mathbf{A}\) si $$\mathbf{A}=\left(\begin{matrix}1&2&5\\3&1&3\\2&4&0\\\end{matrix}\right)$$ Solución: añadiendo las primeras dos columnas para una matriz \(3\times5\) y trazando las diagonales,

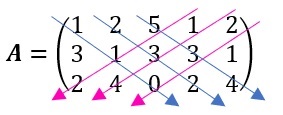
\begin{align} &{\rm det}\mathbf{A}=1\left(1\right)0+2\left(3\right)2+5\left(3\right)4-\left(5\left(1\right)2+1\left(3\right)4+2\left(3\right)0\right)\\ &{\rm det}\mathbf{A}=12+60-(10+12)\\ &{\rm det}\mathbf{A}=72-22=50\end{align} Que es el mismo resultado obtenido mediante la expansión de Laplace en el ejemplo cuatro, lo cual confirma que no importa el método usado para realizar el cálculo, ya que si no se comenten errores el resultado será el mismo.

La enorme diferencia entre este método y la expansión de Laplace radica, en que la regla de Sarrus solo puede ser usado para determinantes \(3\times3\) mientras que la expansión de Laplace constituye en método general, el cual puede ser usado sin importar el orden de la matriz.

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.

Vectores y determinantes.

Un vector es un ente matemático que tiene módulo dirección y sentido, el cual se representa por \(\mathbf{u}=\left(u_1,u_2,u_3\cdots u_n\right)\) en forma de una matriz renglón (o columna si se desea) o en la escritura secular como \(\vec{u}\), ambas notaciones se usarán según convenga en la escritura, donde las cantidades \(u_1,u_2,u_3\cdots u_n\) son llamadas componentes del vector y pueden ser números reales o complejos, según el tipo de variable que se está estudiando.

El modulo o tamaño del vector también llamado magnitud, se define como la raíz cuadrada de la suma de los cuadrados de sus componentes, esto es $$||\vec{\mathbf{u}}||=\sqrt{u_1^2+u_2^2+u_3^2+\cdots+u_n^2}$$ Notación que aunque es parecida a la de determinantes nada tiene que ver con esto puesto que los determinantes solo existen para matrices cuadradas y \( \vec{\mathbf{u}}=\left(u_1,u_2,u_3\cdots u_n\right)\) no lo es.

En términos de las coordenadas espaciales \(x,\ y,\ z,\) se definen los vectores unitarios (de módulo uno) \(\mathbf{i},\mathbf{j},\mathbf{k},\) como, \(\mathbf{i}=\left(1,0,0\right)\) con dirección al eje \(x\) positivo \(\mathbf{j}=\left(0,1,0\right),\) con dirección al eje ye positivo y el vector \(\mathbf{k}=\left(0,0,1\right)\) con dirección al eje \(z\) positivo como se muestra en la figura de la izquierda.

Producto vectorial.
El producto vectorial de dos vectores \(\mathbf{u}\) y \(\mathbf{v}\) denotado como \(\mathbf{u}\times\mathbf{v} \) también llamado producto cruz puede definirse en términos del determinante como sigue. Sean los vectores, $$\mathbf{u}=\left(u_x,u_y,u_z\right)~~ {\rm y}~~ \mathbf{v}=\left(v_x,v_y,v_z\right)$$ los cuales también pueden escribirse en función de los vectores unitarios \(\mathbf{i},\mathbf{j}, \mathbf{k}\) como $$\mathbf{u}=u_x\mathbf{i}+u_y\mathbf{j}+u_z\mathbf{k}~~{\rm y}~~\mathbf{v}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k}$$ entonces el producto vectorial \(\mathbf{u}\times\mathbf{v}\) es, $$\mathbf{u}\times\mathbf{v}=\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\u_x&u_y&u_z\\v_x&v_y&v_z\\\end{matrix}\right|=\left|\begin{matrix}u_y&u_z\\v_y&v_z\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}u_x&u_z\\v_x&v_z\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}u_x&u_y\\v_x&v_y\\\end{matrix}\right|\mathbf{k}$$ Ejemplo. Momento de torsión. el momento de torsión \(\mathbf{\tau}\) (tau) también llamado vector torca, par de torsión o momento de fuerza es un vector el cual “describe” el movimiento de un cuerpo que girar sobre un eje fijo, y está relacionado con los vectores de desplazamiento \(\mathbf{r}\) y el vector fuerza \(\mathbf{F}\) mediante la expresión, \(\mathbf{\tau}=\mathbf{r}\times\mathbf{F}.\) Se aplica una fuerza \(\mathbf{F}=\left(3.0\mathbf{i}+5.0\mathbf{j}\right)N\) sobre un objeto el cual puede girar en torno a un eje fijo en la dirección del eje \(z\). Si la fuerza se aplica en un punto cuya ubicación \(\mathbf{r}\left(7.0\mathbf{i}+7.0\mathbf{j}\right)m\) determinar la magnitud del vector momento de torsión.
Solución: la magnitud del vector torca es \(||\vec{\tau}||=\sqrt{\tau_x^2+\tau_y^2+\tau_z^2}\) y para hallar las componentes se realiza el producto cruz. \begin{align} \vec{\tau}&=\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\7.0&7.0&0.0\\3.0&5.0&0.0\\\end{matrix}\right|\\ \vec{\tau}&=\left|\begin{matrix}5.0&0.0\\2.0&0.0\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}7.0&0.0\\3.0&5.0\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}7.0&7.0\\3.0&5.0\\\end{matrix}\right|\mathbf{k}\\ \vec{\tau}&=\left(35-21\right)\mathbf{k}=14\mathbf{k}Nm\\ \left|\left|\vec{\tau} \right|\right|&=\sqrt{\left(14Nm\right)^2}=14Nm\end{align} Ejemplo Fuerza magnética. La fuerza magnética a la cual es sometida un cuerpo está dada por \(\mathbf{F}=q\mathbf{v}\times\mathbf{B}\) donde \(q\) es la carga, \(\mathbf{v}\) es el vector velocidad y \(\mathbf{B}\) es el vector de campo magnético. Un protón se mueve con una velocidad \(\mathbf{v}=(3\mathbf{i}– 4\mathbf{j}+2\mathbf{k})m/s\) en una región donde el campo magnético es \(\mathbf{B}=(5\mathbf{i}+2\mathbf{j}–3\mathbf{k})T\). ¿Cuál es la magnitud de la fuerza magnética que experimenta esta carga?
Solución: la magnitud de la fuerza está dada por \(\mathbf{F}=q||\mathbf{v}\times\mathbf{B}||\) donde la carga del protón es \(q=1.60\times{10}^{-19}C.\) \begin{align} \mathbf{v}\times\mathbf{B}&=\left|\begin{matrix}\mathbf{i}&\ \ \ \ \mathbf{j}&\ \ \ \mathbf{k}\\3&-4&\ \ \ 2\\5&\ \ \ 2&-3\\\end{matrix}\right|\\ \mathbf{v}\times\mathbf{B}&=\left|\begin{matrix}-4&\ \ 2\\2&-3\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}3&\ \ 2\\5&-3\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}3&-4\\5&\ \ \ \ 2\\\end{matrix}\right|\mathbf{k}\\ \mathbf{v}\times\mathbf{B}&=(8\mathbf{i}+19\mathbf{j}+26\mathbf{k}){\rm T}m/s\\ ||\mathbf{v}\times\mathbf{B}||&=\sqrt{8^2+19^2+26^2}=\sqrt{1101}{\rm T}m/s\\ \mathbf{F}&=q||\mathbf{v}\times\mathbf{B}||=1.60×10^{-19}C (\sqrt{1101}){\rm T}m/s\\ \mathbf{F}&=5.31×10^{-18}{\rm N}\end{align} Ejemplo Área de un paralelogramo. El área de un paralelogramo en unidades cuadradas \(u^2\), cuyos lados adyacentes son los vectores \(\mathbf{u}\) y \(\mathbf{v}\) está dada por \( A=||\mathbf{u}\times\mathbf{v}||.\) Determinar el área del paralelogramo de lados adyacentes \(\mathbf{u}=(2\mathbf{i} + 2\mathbf{j} –4\mathbf{k})\) y \(\mathbf{v}=(-2\mathbf{i} +3\mathbf{j} +\ 4\mathbf{k}).\) \begin{align} \mathbf{u}\times\mathbf{v}&=\left|\begin{matrix}\ \ \ \mathbf{i}&\mathbf{j}&\ \ \ \mathbf{k}\\\ \ \ 2&2&-4\\-2&3&\ \ \ 4\\\end{matrix}\right|\\ \mathbf{u}\times\mathbf{v}&=\left|\begin{matrix}2&-4\\3&\ \ \ 4\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}\ \ \ 2&-4\\-2&\ \ \ 4\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}\ \ \ 2&2\\-2&3\\\end{matrix}\right|\mathbf{k}\\ \mathbf{u}\times\mathbf{v}&=20\mathbf{i}+10\mathbf{k}\\ A&=\left|\left|\mathbf{u}\times\mathbf{v}\right|\right|=\sqrt{{20}^2+{10}^2}\\ A&=10\sqrt{5}u^2\end{align} Como puede notar existen diversas aplicaciones para un determinante de orden \(3\times3\) estos son solo algunos de los múltiples ejemplos que puede encontrar al estudiar física o matemáticas. Aun queda mucho por conocer.

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.