Álgebra básica de matrices.
Una matriz es un arreglo rectangular en forma de filas y columnas, de entes llamados entradas o elementos de la matriz, representada con una letra mayúscula (por lo general en negritas) de la forma \(\mathbf{A}=\left[a_{ij}\right]\) donde \(i\) representa la iésima fila y \(j\) la j-ésima columna, escrita en la forma, $$\mathbf{A}=\left(\begin{matrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\cdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\\\end{matrix}\right)$$ La notación en negrita se dejará para el estudio de los espacios vectoriales y en su lugar se referirá a una matriz \(\mathbf{A}\) solamente como A.
Las cantidades \(a_{11},\ a_{21},\ldots,a_{mn}\) son llamadas elementos de la matriz y su uso se justifica para facilitar la presentación y el cálculo de datos o entes matemáticos, que a menudo son de gran tamaño, sobre todo en el mundo empresarial y dentro del campo de las ciencias, además no importa si usa, paréntesis, corchetes, al escribir.
Matrices y representación de datos.
A menudo las matrices son usadas para la representación de datos a modo de tablas en los procesos industriales, económicos y científicos, por ejemplo, en el taller textil "Aurora" se fabrican tres tipos de T-shirt tamaño S, M y L, el mismo consta con tres líneas de producción las cuales se encargan del proceso de fabricación de los T-shirt. El mes pasado la producción para cada línea fue de 300S, 400M y 250L, para la línea uno, 400S, 500M, y 300L, para la dos y 450S, 550M y 300L para la tres. Tabulando los datos de manera organiza, la producción se puede representar mediante la matriz,
$$P=\left(\begin{matrix}S&M&L\\300&400&250\\400&450&300\\450&550&300\\\end{matrix}\right) {\rm o\ simplemente}\ P=\left(\begin{matrix}300&400&250\\400&450&300\\450&550&300\\\end{matrix}\right)$$
Observe que, en la segunda matriz, los datos de la primera columna representan las cantidades fabricadas de T-shirt tamaño S, los de la segunda la cantidad T-shirt tamaño M y los de la tercera la producción para el tamaño L. La diferencia entre ambas presentaciones radica en la cantidad de entradas, en el primer caso hay doce entradas (elementos) y en el segundo caso hay tres, el número de entradas determina el orden o dimensión de la matriz.
Orden o dimensión.
Todas las matrices poseen un orden o dimensión, que expresa el número de renglones (filas) y el número de columnas, escrito por convención \(m\times n.\) Así dada las matrices,
$$A=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\\\end{matrix}\right)\ \ \ \ \ \ B=\left(\begin{matrix}u_{11}&u_{12}&u_{13}\\u_{21}&u_{22}&u_{23}\\\end{matrix}\right)\ \ \ \ \ D=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right)$$
\(A\) es de orden \(3\times2, \ \ B\) es de orden \(2\times3, \ \ D\) es de orden \(3\times3.\) Los subíndices en los elementos representan el lugar donde se encuentra el elemento, así si se escribe \(a_{23}\) quiere decir el elemento que está en la fila dos y la columna tres.
Si una matriz es de orden \(n\times n\) (igual número de filas que columnas) como la matriz \(D\) se dice que es una matriz cuadrada.
Aunque en la práctica no es muy común referirse a una matriz de orden \(1\times1\) una matriz \(A=(a_{ij})\) la cual posee una sola entrada, es una matriz \(1\times1.\)
Matriz fila y matriz columna.
Se dice que una matriz \(A\) de orden \(1\times n\) es una matriz fila (también llamada matriz renglón) o vector renglón, mientras que una matriz \(B\) de orden \(m\times1\) es una matriz columna (o vector columna).
$$A=\left(\begin{matrix}a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\\end{matrix}\right)\ \ \ \ \ \ \ \ \ B=\left(\begin{matrix}u_{11}\\u_{21}\\u_{31}\\\vdots\\u_{m1}\\\end{matrix}\right)$$
Para más contenidos y luego clic en la pestaña del contenido deseado.
Matriz transpuesta.
Sea \(A\) una matriz de orden \(m\times n\) entonces la matriz de orden \(n\times m\) denota por \(A^T\) es la matriz transpuesta de \(A\), esto es, \(A^T\) es la matriz que resulta de intercambiar las filas por las columnas de la matriz \(A.\)
$$A=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\\\end{matrix}\right)\ \ \Longrightarrow A^T=\left(\begin{matrix}a_{11}&a_{21}&a_{31}\\a_{12}&a_{22}&a_{32}\\\end{matrix}\right)$$
Ejemplo. Dada la matriz
$$A=\left(\begin{matrix}1&2\\3&4\\5&6\\\end{matrix}\right)\Longrightarrow A^T=\left(\begin{matrix}1&3&5\\2&4&6\\\end{matrix}\right)$$
Igualdad de matrices.
Dos o más matrices son iguales si y solo si, son del mismo orden y los elementos que ocupan posiciones homólogas son iguales, es decir, si,
$$A=\left(\begin{matrix}a&b&c\\x&y&z\\w&u&v\\\end{matrix}\right)\ \ \ \ \ {\rm y} \ \ \ \ \ B=\left(\begin{matrix}1&2&3\\4&5&6\\7&8&9\\\end{matrix}\right)$$
son iguales entonces, \(a=1,\ b=2,\ \ c=3,\ \ x=4\) y así sucesivamente.
Matriz nula.
Se dice que una matriz es nula de dimensión \(m\times n\) cuando cada uno de sus elementos son ceros, por ejemplo,
$$A=\left(\begin{matrix}0&0\\0&0\\\end{matrix}\right)\ \ \ \ B=\left(\begin{matrix}0&0&0\\0&0&0\\\end{matrix}\right)\ \ \ \ D =\left(\begin{matrix}0&0&0\\0&0&0\\0&0&0\\\end{matrix}\right)$$
son todas matrices nulas, de sus respectivos órdenes.
Dentro del mundo de las matrices la matriz nula del orden correspondiente es interpretado como el cero de ese orden y al igual que al trabajar con números este posee cierta propiedades las cuales se verán más adelante al trabajar las operaciones con matrices.
Por otra parte, en física las matrices juegan un papel importantísimo para la explicación y análisis de ciertos fenómenos, sobre todos las matrices cuadradas (orden \(n\times n\)) por lo cual gran parte del análisis aquí presentado está centrado en el estudio de las matrices cuadradas.
Algunas matrices cuadradas especiales.
Para iniciar el apartado se recuerda que una matriz cuadrada es aquella que posee igual número de filas que de columnas, así, por ejemplo,
$$A=\left(\begin{matrix}u&v\\w&x\\\end{matrix}\right)\ \ \ \ \ B=\left(\begin{matrix}1&2&3\\4&5&6\\7&8&9\\\end{matrix}\right)\ \ \ \ \ \ D=\left(\begin{matrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\\\end{matrix}\right)$$
son todas matrices cuadradas, \(A\) es de orden \( 2\times2, \ \ B\) es de orden \(3\times3\)
y \( D\) es de orden \(4\times4.\)
En toda matriz cuadrada se pueden trazar diagonales primarias y diagonales secundarias. Se dice que una diagonal primaria es una diagonal trazada desde un elemento superior izquierdo hasta un elemento inferior derecho, mientras que una diagonal secundaria es una diagonal trazada desde un elemento superior derecho hasta un elemento inferior izquierdo. Una diagonal que comienza en el elemento \(u_{11}\) es simplemente llamada la diagonal principal, y una diagonal que comienza en el elemento \(u_{1n}\) es llamada la diagonal secundaria.
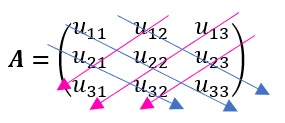
Las diagonales en azul son las diagonales primarias, mientras que las diagonales en rosa son las secundarias. La diagonal principal es aquella que pasa por los elementos \(u_{11},u_{22},u_{33}\) mientras que la diagonal secundaria es aquella que pasa por los elementos \(u_{13},\ u_{22},\) y \(u_{31}.\)
Matriz diagonal
Se dice que una matriz cuadrada es una matriz diagonal cuando todos los elementos por debajo y por encima de la diagonal principal son ceros, así las matrices,
$$A=\left(\begin{matrix}u_{11}&0\\0&u_{22}\\\end{matrix}\right)\ \ \ \ \ \ \ \ \ \ B=\left(\begin{matrix}u_{11}&0&0\\0&u_{22}&0\\0&0&u_{33}\\\end{matrix}\right)$$
son matrices diagonales. Se suele escribir una matriz diagonal \(A\) como \(A={\rm diag}\{u_{11},u_{22}\}\) como \(B={\rm diag}\{u_{11},u_{22},u_{33}\}.\)
Si en una matriz diagonal sus elementos son todos iguales se llama matriz escalar, si son todos unos, se le llama matriz identidad de ese orden, por ejemplo, $$A=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\ \ \ B=\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)$$ son las matrices identidad de orden \(2\times2\) y \(3\times3\) respectivamente y se denotan como \(I_2,~ I_3.\) Las matrices identidad juegan un papel importante en algunas de las operaciones con matrices y en la resolución de sistemas de ecuaciones lineales mediante el empleo de matrices. Para las matrices $$D=\left(\begin{matrix}3&0&0\\0&3&0\\0&0&3\\\end{matrix}\right)\ \ E=\left(\begin{matrix}3&0&0\\0&5&0\\0&0&7\\\end{matrix}\right)$$ \(D\) es una matriz escalar, y la matriz \(E\) solo es diagonal.
Matriz simétrica.
Se dice que una matriz cuadrada \(A\) es simétrica si \(A^T=A,\) es decir, \(a_{ij}=a_{ji}\) y por tanto es simétrica respecto a su diagonal principal, esto es,
$$A=\left(\begin{matrix}u_{11}&u_{12}&u_{13}\\u_{12}&u_{22}&u_{23}\\u_{13}&u_{23}&u_{33}\\\end{matrix}\right)\ {\rm por\ ejemplo}\ A=\left(\begin{matrix}2&7&-11\\7&3&4\\-11&4&5\\\end{matrix}\right)$$
Matriz antisimétrica.
Se dice que una matriz \(A\) tal que \(A^T=-A\) es antisimétrica. Si \(A\) es antisimétrica entonces tiene la forma,
$$A=\left(\begin{matrix}0&a_{12}&\cdots&a_{1n}\\-a_{12}&0&\cdots&a_{2n}\\\vdots&\cdots&\ddots&\vdots\\-a_{1n}&a_{2n}&\cdots&0\\\end{matrix}\right)\ {\rm por\ ejemplo}\ A=\left(\begin{matrix}0&7&-11\\-7&0&4\\11&-4&0\\\end{matrix}\right)$$
Matrices triangular superior e inferior.
Se dice que una matriz cuyo elementos son todos ceros por debajo de su diagonal principal es una matriz triangular superior, mientras que una matriz cuyos elementos por encima de la diagonal principal son todos ceros es una matriz triangular inferior.
$$A=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{31}\\\end{matrix}\right)\ \ \ \ \ \ \ \ \ \ \ B=\left(\begin{matrix}u_{11}&0&0\\u_{21}&u_{22}&0\\u_{31}&u_{32}&u_{31}\\\end{matrix}\right)$$
La matriz \(A\) es triangular superior, mientras que \(B\) es triangular inferior.
Matriz compleja conjugada.
Sea \(A\) una matriz no nula, entonces la matriz compleja conjugada de \(A\) denotada por \(A^\ast\) es la matriz de que resulta de tomar el conjugado complejo de cada uno de los elementos de la matriz \(A\).
Ejemplo. Determinar la matriz conjugada compleja de, $$A=\left(\begin{matrix}2i&3&-5i\\2-3i&1&1+i\\\end{matrix}\right)$$ Solución: aplicando la definición de matriz conjugada compleja, $$A^\ast=\left(\begin{matrix}-2i&3&5i\\2+3i&1&1-i\\\end{matrix}\right)$$ Es claro que, si todos los elementos de una matriz son reales, la matriz compleja conjugada es igual a la matriz dada, por ser el conjugado de un número real el mismo número real.
Matriz conjugada hermitiana o adjunta.
Se dice que, dada una matriz \(A\) no nula, la matriz conjugada hermitiana denotada por \(A^\dagger\) es la matriz transpuesta de la matriz compleja conjugada o de manera equivalente la compleja conjugada de su transpuesta.
$$A^\dagger={(A^\ast)}^\dagger={(A^T)}^\ast$$
Si \(A\) es una matriz real, como ya se ha visto \(A^\ast=A\) y por tanto \(A^\dagger=A^T.\) Además, dado un producto de varias matrices su conjugada hermitiana cumple la condición,
$$\left(ABC\ldots Z\right)^\dagger=Z^\dagger\ldots C^\dagger B^\dagger A^\dagger$$
Note la similitud entre esta expresión y la expresión para la transpuesta de un producto (puede ver la en la pestaña de multiplicación).
Ejemplo: Determinar la matriz conjugada hermítica para la matriz, $$\mathbf{A}=\left(\begin{matrix}2&3i\\2+3i&3-2i\\5&i\\\end{matrix}\right)$$ Solución: de la definición \(\mathbf{A}^\dagger={(\mathbf{A}^\ast)}^\dagger\) entonces, $$\mathbf{A}^\dagger=\left(\begin{matrix}2&-3i\\2-3i&3+2i\\5&-i\\\end{matrix}\right)^T=\left(\begin{matrix}2&2-3i&5\\-3i&3+2i&-i\\\end{matrix}\right)$$
