Aritmética
Aritmética es la rama de la Matemática que estudia los números y las operaciones hechas con ellos.
En cuanto a los números, la aritmética considera dos tipos, los números primos (enteros \(p\) mayores que uno, cuyos únicos divisores positivos son el uno y el mismo número \(p\)) y los números compuestos (todos los que no son primos y por tanto, tienen divisiores distintos de ellos mismos).
Para los divisores de un número se dice que un número entero divide a otro entero, cuando al realizar la división, esta es exacta (el residuo es cero).
En cuanto a las operaciones, la artimética considera siete operaciones fundamentales, potenciación, radicación, división, multiplicación, adición, sustracción, y logaritmación, las primeras seis se estudian en la educación primaria y la logaritmación se añade en la secundaria.
Operaciones básicas y su jerarquía.
Al igual que en la vida cotidiana en aritmética los números representan cantidades conocidas de algo, por ejemplo, al decir cinco naranjas, el número 5 representa la cantidad de naranjas que se tiene, no tiene significado expresar que se tiene o debe cinco, si no se dice la unidad, completar la idea con la unidad resulta de gran importancia para la compresión de la vida y el estudio de las ciencias. Así al hablar de cinco kilómetros, se escribe \(5km\), donde cinco es la cantidad y \(km\) es la unidad de longitud.
Al trabajar con los números como ya se ha dicho se han de considerar siete operaciones fundamentales, sin embargo, cabe destacar que al trabajar con ejercicios donde se tiene más de una operación, existe un orden que debe ser respetar si desea resultados correctos.
Aunque pueda parecer simple, un error común que se debe evitar al trabajar en matemáticas es tener resultados erróneos por no tomar en cuenta el orden operacional, es por esto que, este estudio se inicia presentando estas simples, pero necesarias reglas operacionales para obtener resultados correctos.
El orden operacional.
El orden operacional también llamado jerarquía de las operaciones, son una serie de reglas establecidas por los matemáticos, con el fin de lograr los resultados correctos al trabajar con operaciones combinadas. Dicho orden se resume a continuación.
Orden de las operaciones
1. Operaciones dentro de signos de agrupación (o bajo un signo radical).
2. Potenciación 3. Radicación.
4. División. 5. Multiplicación.
6. Adición o sustracción.
La logaritmación que se estudiará más adelante tiene el mismo orden que la potenciación, además, se deben recordar algunos aspectos importantes de estas operaciones, estos se muestran a continuación, con la finalidad de recordar al lector los nombres de los elementos de las operaciones básicas.
Propiedades de la adición.
Sean \(a,\ b,c\) elementos cualquieras de \(\mathbb{R}\), si \(a+b=c\) los números \(a\) y \(b\) son llamados sumandos y \(c\)es la suma o total, bajo la acción de la operación de adición se verifican las siguientes propiedades:
Conmutativa expresa que el orden de los sumandos no altera la suma esto es \(a+b=b+a\) (no importa el orden al sumar). Cabe destacar que esta propiedad se cumple solo bajo ciertas condiciones que se estudiarán al analizar sumas infinitas de sucesiones decrecientes.
Asociativa expresa que se pueden agrupar los sumandos en la manera que se deseé y la suma o total no se altera, esto es,
$$a+b+c=\left(a+b\right)+c=a+\left(b+c\right)=b+(c+a).$$
Modular o del elemento neutro. Existe un único número (el cero), el cual al ser sumado con cualquier otro número \( \mathbb{R},\) da como resultado el mismo número \(\mathbb{R},\) esto es \(a+0=a;\ \ b+0=b.\)
Inverso aditivo. Existe un número \(\mathbb{R}_2\) que al ser sumado que otro \(\mathbb{R}_1\) da como resultado el elemento neutro. Si \(\mathbb{R}_1+\mathbb{R}_2=0\) entonces se dice que \(\mathbb{R}_2\) y \(\mathbb{R}_1\) son inversos aditivos.
Operación inversa. La adicción tiene por operación inversa la resta o sustracción en la cual si \(a-b=r\) el número \(a\) es el minuendo, \(b\) es el sustraendo y \(r\) es el resta o diferencia.
Multiplicación.
La multiplicación es una operación que tiene por objeto dadas dos o más cantidades llamadas factores, hallar otra cantidad llamada producto. Sean \(a,b,c,p\) elementos cualquieras de \(\mathbb{R},\) si \(ab=p\) los números \(a\) y \(b\) son llamados factores y \(p\) es el producto bajo la operación de multiplicación se verifican las siguientes propiedades:
Conmutativa: el orden de los factores no altera el producto, esto es a\cdot b=b\cdot a (no importa el orden).
Asociativa: se pueden agrupar los factores como se desee y el producto no se altera, esto es $$a\cdot b\cdot c=\left(b\cdot a\right)\cdot c=\left(a\cdot c\right)\cdot b=a\cdot(b\cdot c)$$
Distributiva con respecto de la adición o la sustracción. si \(a,b,c\) son elementos de \(\mathbb{R},\) se verifica que:
\begin{align}
&1.~~a\left(b+c-m\cdots\right)=ab+ac-am\cdots\\
&2.~~\left(m+n+\cdots\right)\left(a+b-c\cdots\right)=m\left(a+b-c\cdots\right)+n\left(a+b-c\cdots\right)+\cdots\end{align}
Modulativa o elemento neutro. Existe un único número (el uno) que al ser multiplicado con un \mathbb{R} cualquiera, da como resultado el mismo número \(\mathbb{R},\) esto es \( 1\cdot\mathbb{R}=\mathbb{R}\cdot1=\mathbb{R}\)
Inverso multiplicador o reciproco: Existe un único número denotado por r tal que \(a\cdot r=1.\) Al estudiar las operaciones con fracciones se verá cómo encontrar este número.
Propiedad del elemento absorbente. Existe un único número (el cero) tal que, al multiplicar un número \(\mathbb{R}\) cualquiera por él, el resultado es cero. \(\mathbb{R}\times0=0\times\mathbb{R}=0.\)
Operación inversa: Si \(n\div d=c+r\) el número \(n\) llamado dividendo, el número \(d\) es llamado divisor, \(c\) es el cociente y \(r\) es el residuo. Si para una división cualquiera se tiene,
\begin{align}\frac{n}{d}=c+\frac{r}{d}\end{align}
el número \(n\) llamado numerador, es el dividendo, el número \(d\) llamado denominador es el divisor, \(c\) es el cociente y \(r\) es el residuo.
Si \(r=0\) la división es exacta, si \(r\neq0\) la división es entera.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Conjuntos numéricos.
Un conjunto numérico es una "agrupación" de números con ciertas características que permiten identificarlos (al estudiar teoría de conjunto más adelante profundizará en el concepto de conjunto). Por lo general los conjuntos se representa por una letra mayúscula escribiendo entre llaves sus elementos con minúsculas. Los conjuntos numéricos no tienen final (son infinitos).
Notación de pertenencia.
Sobre un algo cualquiera llamado \(k\) y un conjunto \(A\) se puede decir una de dos cosas:
\begin{align}
&1.~~k\in A~~~~(k~ \mathrm{pertenece~ a}~ A).\\
&2.~~k\notin A~~~~(k~ \mathrm{no~pertenece~ a}~ A).
\end{align}
Por ejemplo, si \(A\) representa al conjunto de los números pares, se puede escribir, \(6\in A\) (seis pertenece a A) y \(7\notin A\) (siete no pertenece a \(A\)).
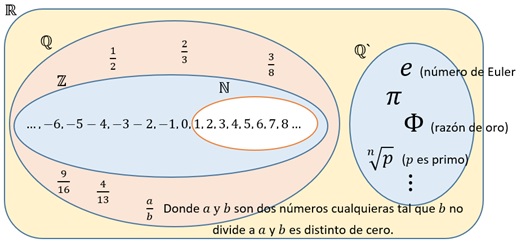
Números naturales \(\mathbb{N}\).
El conjunto de los números naturales \(\mathbb{N}\) es el conjunto formado por los números utilizados para contar o representar el orden de las cosas y es el único conjunto numérico que tiene un comienzo.
$$\mathbb{N}=\left\{1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10,\ \ldots\right\}$$
Números enteros \(\mathbb{Z}\).
Con los números naturales era imposible representar la inexistencia de algo ¿cómo representar qué no se tiene algo? Mediante el uso del “cero” se pudo resolver este problema, pero había aun un problema ¿cómo representar deudas o pérdidas? Para esto se hizo necesario ampliar el conjunto de los números naturales, así se estableció el uso de “números negativos” los cuales representaban que se debía una cantidad inversa al que el número representaba. Así que los números enteros \(\mathbb{Z}\) son la unión del conjunto de los números naturales, el cero y los inversos de los naturales. No existe un primer número entero, ni un último, de donde se tiene que:
$$\mathbb{Z}=\{\ldots,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,\ldots\}$$
así se puede indicar que \(100\ \in\mathbb{Z}\) mientras que \(0.33\notin\mathbb{Z}\)
Conjunto de los Racionales \(\mathbb{Q}\).
El conjunto de los números racionales \(\mathbb{Q}\) es el conjunto de todos los números que se pueden expresar como el cociente de dos enteros (resultado de una división) por lo que contine todas las fracciones matemáticas posibles que se pueden escribir al junto de los enteros \(\mathbb{Z}\) y por tanto, a los naturales \(\mathbb{N}.\)
$$\mathbb{Q}=\left\{\frac{n}d,\mathbb{Z}\right\}$$
donde \(n/d\) es cualquier fracción posible.
Conjunto de los números irracionales \(\mathbb{Q'}\)
El conjunto de los números irracionales \(\mathbb{Q'}\) (cu prima) es el conjunto de los números que no pueden ser expresados como el cociente de dos enteros.
El número irracional más conocido es el número \(\pi\), además de este, otros dos números irracionales muy conocidos son el número de Euler (número \(e\)) y la famosa razón de oro representada por \(\Phi\) (phi). Dentro de \(\mathbb{Q'}\) están todas las raíces de todos los números primos.
$$\mathbb{Q}^\prime=\left\{\sqrt p,\ \pi\ ,e,\Phi,\ ...\right\}$$
donde \(p\) es un número primo.
Conjunto de los números reales \(\mathbb{R}\).
El conjunto de los números reales \(\mathbb{R}\) es un "superconjunto" que contiene a todos los conjuntos anteriores mencionados.
Posee la propiedad de completitud o continuidad también llamada propiedad de densidad establece que "entre dos números reales cualquiera hay infinitos número reales" la cual permite representar los reales como una recta continua de puntos en un sistema coordenado (a cada punto le pertenece un número y a cada número le pertenece un punto). Existe otro tipo conjunto numérico llamado el conjunto de los números complejos el cual será estudiando más adelante. A continuación, se muestra una representación gráfica de los reales.
Operaciones en los reales.
Se dice que una operación aritmética es interna en un conjunto dado, si el resultado bajo la acción de la operación al operar dos números que pertenecen al conjunto también pertenece al conjunto. La división no es interna en los conjuntos \( \mathbb{N},\mathbb{Z},\) y \(\mathbb{R}.\)
Ejemplo 1. Determinar el valor de
\(20\times20\div20+40-4\div2^2+\sqrt{3^4}\)
Solución: sea \(S\) el resultado de las operaciones entonces,
\begin{align}
&S=\ 20\times20\div20+40-4\div4+\sqrt{81}\\
&S=20\times20\div20+40-4\div4+9\\
&S=20\times1+40-1+9\\
&S=20+40-1+9\\
&S=68~~~~ \mathrm{Simplificando.}\\
\end{align}
Ejemplo 2. Determinar la suma de \(10+\left\{5\left(2-8\right)\right\}\)
Solución sea \(S\) la suma buscada, entonces,
\begin{align}
&S=10+5{-6}
&S=10-30=-20\end{align}
Ejemplo 3. Determinar la suma de \(25-\left(12-\left(5+8\cdot3\right)-\sqrt{20\cdot10+25}\right)\)
solución: sea \(S\) la suma buscada, entoces se tiene,
\begin{align}
&S=25-\left(12-29-15\right)\\
&S=25-\left(-32\right)=57\end{align}
Ejemplo 4. Determinar la suma de \(-2(3{4\times15+21}-\sqrt[3]{16\div4+4})+17\)
Solución: sea \(S\) la suma buscada, entonces,
\begin{align}
&S=-2(3{60+21}-\sqrt[3]{8})+17\\
&S=-2(243-2)+17\\
&S=-2(241)+17\\
&S=-465\end{align}
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Definición de valor absoluto: el valor absoluto de una cantidad \(c\) denotado como \(\left|c\right|\) se define como, $$\left|u\right|=\left\{\begin{array}1 -u~~~\mathrm{si}~ u < 0\\ ~~u~~~\mathrm{si}~ u \geq 0 \end{array}\right.$$ Además, si \(n\) es par en \(\sqrt[n]{u^n}\) entonces \(\sqrt[n]{u^n}=\left|u\right|\).
El valor absoluto de una cantidad \(u\) no considera el signo, y puede interpretarse como la distancia en la recta real desde \(u\) hasta el cero. así por ejemplo se tiene que, $$\left\{\begin{array}{l} \left|-5\right|=-(-5)=5\\ \left|5\right|=5~~~~~~~~~~~~~~\\ \end{array}\right.$$ de donde se infiere que el valor absoluto no considera el signo y por tanto, siempre es positivo.
Algunas propiedades del valor absoluto.
1. \(\left|u\right|\geq0~~~~\) (nunca es negativo).
2. \( \left|u\right|=0\Longleftrightarrow u=0.\)
3. \(\left|uv\right|=\left|u\right|\left|v\right|~~~~\) Valor absoluto de un producto.
4. \(|u/v|=|u|/|v|~~~~\) Valor absoluto de un cociente.
5. \(|u|^n=u^n\) si \(n\) es par.
6. \(\sqrt[n]{u^n}=\left|u\right|\) si \(n\) es par (segunda definición dada).
Aunque existen otras propiedades para el valor absoluto, estás deben esperar a la utilización de resoluciones de desigualdades para ser analizadas.
