La radicación se define como la operación básica de la aritmética inversa a la potenciación, consiste en dada una potencia (cantidad sub radical o radicando) y el exponente a la cual está elevada (índice radical), hallar la base de dicha potencia. A continuación se presentasn los elementos de la radicación.
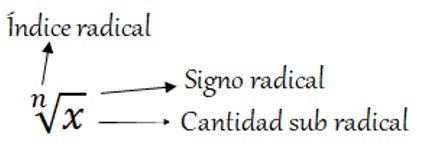
La radicación puede interpretarse como sigue:
Dada la cantidad subradical \(x\) se debe determinar otra cantidad \(C\) la cual al ser elevada al indice \(n\) da como resultado la cantidad \(x\) esto es, si \(\sqrt[n]x=C\) entonces \(C^n=x.\) Escribir \(\sqrt[n]{x}\) y quiere decir ¿Cuál es el número que elevado a \(n\) da como resultado \(x\)?
Si el índice radical es dos, la operación de radicación se llama raíz cuadrada y el índice radical no se escribe. Si el índice es tres se llama raíz cúbica, si es cuatro raíz cuarta y así sucesivamente. $$\sqrt{x}~~~~Se~lee~raíz~cuadrada~de~x.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ $$\sqrt[3]{x}~~~~Se~lee~raíz~cúbica~de~x.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ $$\sqrt[4]{x}~~~~Se~lee~raíz~cuarta~de~x.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ $$\sqrt[5]{x}~~~~Se~lee~raíz~cuadrada~de~x ~ y~ así~sucesivamente.$$ A continuación se presenta en forma de tabla algunos de los ejemplos más comunes de la radicación, junto a los razonamientos que conducen al resultado.
Forma radical |
Resultado |
Razón |
|---|---|---|
$$\sqrt4$$ |
$$2$$ |
$$2^2=4$$ |
$$\sqrt[3]{27}$$ |
$$3$$ |
$$3^3=27$$ |
$$\sqrt[4]{625}$$ |
$$5$$ |
$$5^4=625$$ |
$$\sqrt[5]{32}$$ |
$$2$$ |
$$2^5=32$$ |
En la práctica matemática, se trabajan las raíces cuadradas (índice dos) y cúbicas (índice tres) con mayores frecuencias que todas las demás, por tanto, el estudio de raices se centra en éstos tipos.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Propiedades de los radicales.
Sean \(a,~ b,~m.~n,\) y \(x\) números reales positivos, entonces bajo la operación de radicación se cumplen las propiedades siguientes: $$1.~~\sqrt[n]{x^m}=x^{\frac{m}{n}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Un\ radical\ puede\ escribirse\ como\ un\ exponente.$$ $$2.~~\sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Propiedad\ distributiva\ con\ la\ multiplicación.~~~~$$ $$3.~~\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Propiedad\ distributiva\ con\ la\ división.~~~~~~~~~~~~~~~$$ Aunque algunos autores escriben otras propiedades para la radicación, basta con éstas tres ya que si entiende la propiedad uno \(\sqrt[n]{x^m}=x^{\frac{m}{n}}\) por extención puede aplicar cualquier propiedad de los radicales que necesite.
Tenga cuidado al trabajar con números negativos, ya que la radicación de indice par no está definida para ellos, y además en este conjunto \(\mathbb{R}^-\) no se cumplen del todo las propiedadas mencionadas al trabaja con números negativos.
Otro elemento importante a tener en cuenta es si se está o no trabajando en el conjunto de los números complejos \(\mathbb{C}\), estos tienen sus propias prodiedades, y aunque en algunos casos coincidan con las de los reales, no intente trabajar radicación de números complejos, como si fueran reales.
Para ver el uso de las propiedades de los radicales y como éstas ayudan en la resolución de ejercicios con radicales, has clic en la pestaña de ejercicios y análiza los ejercicios resueltos.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Racionalización.
La racionalización en el contexto matemático se refiere a escribir una cantidad en forma racional. Por lo general consiste en remover radicales del denominador (o el numerador) de una fracción a través de procedimientos algebraicos.
Por acuerdo los matemáticos han establecidos no dejar una respuesta en la medida de los posible con radicales en el denominador y para tales fines se realiza la racionalización mediante operaciones de multiplicación y división para escribirlo como una cantidad racional.
Aunque en la mayoría de los casos la racionalización se hace con el denominador de una expresión, en el estudio del Cálculo muchas veces es necesario racionalizar el numerador de una expresión para la determinación del límite de una función, es por esta razón que se deben estudiar técnicas de racionalización tanto para denominadores como numeradores. La racionalización está basada en los siguientes artificios matemáticos fundamentales.
1. Propiedad del elemento neutro de la multiplicación.
2. Producto de binomios conjugados \(\left(u+v\right)\left(u-v\right)=u^2-v^2\)
3. Propiedades de los exponentes.
4. Propiedades de los radicales.
5. Binomio de Newton para casos avanzados.
Estos hacen posible escribir la expresión en una forma acomodada, según el caso de estudio para el trabajo que se desea efectuar, como se ilustra en los siguiente ejemplos.
Ejemplo 1. Racionalizando una raíz cuadrada simple. Sean \(c\in\mathbb{R}\) y \(x\in\mathbb{R}^+\) racionalizar \(c/\sqrt x.\)
Solución: Usando la propiedad de elemento neutro de la multiplicación para multiplicar por un “uno acomodado” igual a \(\sqrt{x} /\sqrt{x}\) se tiene,
$$
\frac{c}{\sqrt x}\ \ =\frac{c}{\sqrt x}\ \frac{\sqrt x}{\sqrt x}=\frac{c\sqrt x}{x}$$
Lo cual muestra que, para todo \(c\) y \(x\in\mathbb{R}^+\) la expresión \(c/\sqrt{x}\) puede escribirse como,
$$\frac{c}{\sqrt x}\ \ =\frac{c\sqrt x}{x}$$
de donde se pueden inferir resultados como,
\begin{array}{c c c}
a)\frac{3}{\sqrt5}=\frac{3\sqrt5}{5}&b)\frac{5}{2\sqrt7}=\frac{5\sqrt7}{2(7)}=\frac{5\sqrt7}{14}&c)\frac{7}{3\sqrt{11}}=\frac{7\sqrt{11}}{33}\end{array}
Ejemplo 2. Racionalizando raíces enésimas. Sean \(c\in\mathbb{R}\) y \(x\in\mathbb{R}^+\) racionalizar \(c/\sqrt[n]{x^m}.\)
Solución: comience por escribir \(\sqrt[n]{x^m}=x^{m/n},\) y luego multiplique por un “uno acomodado”, que para este caso es de la forma \(x^{1-m/n}/x^{1-m/n}.\)
\begin{align}
&\frac{c}{\sqrt[n]{x^m}}=\frac{c}{x^{m/n}}\left(\frac{x^{1-m/n}}{x^{1-m/n}}\right)\\
&\frac{c}{\sqrt[n]{x^m}}=\frac{cx^{1-m/n}}{x}\end{align}
del anterior ejemplo se concluye el importante resultado
$$\frac{c}{\sqrt[n]{x^m}}=\frac{cx^{1-m/n}}{x}$$
El ejemplo uno es un caso particular de este caso, otros ejemplos de este caso se presentan a continuación.
Ejemplo 3. Racionalizar las cantidades:
$$\begin{array}{c c c}
a)\ \frac{100}{\sqrt[3]{2^9}}&b) \ \frac{7}{\sqrt[2]{5^3}}&c)\ \frac{11}{\sqrt[5]{3^2}}\end{array}$$
Solución: multiplicando por un “uno acomodado” en cada caso se tiene,
\begin{align}
&a)\ \ \frac{100}{\sqrt[3]{2^9}}=\frac{100}{2^{9/3}}=\frac{100}{2^3}=\frac{100}{8}=\frac{25}{2}\\
&b)\ \frac{7}{\sqrt[2]{5^3}}=\frac{7}{\sqrt{5^2(5)}}=\frac{7}{5\sqrt5}=\frac{7\sqrt5}{5(5)}=\frac{7\sqrt5}{25}\\
&c)\ \frac{11}{\sqrt[5]{3^2}}=\frac{11}{3^{2/5}}\left(\frac{3^{3/5}}{3^{3/5}}\right)=\frac{11(3^{3/5})}{3}=\frac{11\sqrt[5]{3^3}}{3}\end{align}
Ejemplo 4. Racionalizando sumas o diferencia con raíces cuadradas. Racionalizar las expresiones.
$$a)\frac{5}{2+\sqrt3}\ \ \ \ \ \ \ b)\frac{13}{7-\sqrt{11}}$$
Solución: se multiplica numerador y denominador de ambas expresiones por el conjugado del denominador (un uno acomodado), para tener la expresión \(\left(u+v\right)\left(u-v\right)=u^2-v^2\) (diferencia de cuadrados).
Solución a:
\begin{align}
&\frac{5}{2+\sqrt3}\left(\frac{2-\sqrt3}{2-\sqrt3}\right)
=\frac{5(2-\sqrt3)}{(2+\sqrt3)(2-\sqrt3)}\\
&\frac{5}{2+\sqrt3}\left(\frac{2-\sqrt3}{2-\sqrt3}\right)=\frac{5(2-\sqrt3)}{4-3}=10-5\sqrt3\end{align}
Solcuión b:
\begin{align}
&\frac{13}{7-\sqrt{11}}\left(\frac{7+\sqrt{11}}{7+\sqrt{11}}\right)=\frac{13\left(7+\sqrt{11}\right)}{\left(7-\sqrt{11}\right)\left(7+\sqrt{11}\right)}\\
&\frac{13}{7-\sqrt{11}}\left(\frac{7+\sqrt{11}}{7+\sqrt{11}}\right)=\frac{91+13\sqrt{11}}{38}\end{align}
Ejemplo 5. Expresiones algebraicas. Racionalizar las expresiones,
$$a)\frac{5x}{\sqrt{x-4}-3}\ \ \ \ \ \ \ \ \ \ \ \ \ \ b)\frac{x+3}{7-\sqrt{2x-6}}$$
Solución: multiplicando numerador y denominador por el conjugado del de nominador y realizando las operaciones planteadas, para la solución a se tiene
\begin{align}
&\frac{5x}{\sqrt{x-4}-3}=\frac{5x}{\sqrt{x-4}-3}\ \left(\frac{\sqrt{x-4}+3}{\sqrt{x-4}+3}\right)\\
&\frac{5x}{\sqrt{x-4}-3}=\frac{5x(\sqrt{x-4}+3)}{x-4-9}\\
&\frac{5x}{\sqrt{x-4}-3}=\frac{5x\sqrt{x-4}+15x}{x-13}\end{align}
Solución b:
\begin{align}
&\frac{x+3}{7-\sqrt{2x-6}}=\frac{x+3}{7-\sqrt{2x-6}}\ \left(\frac{7+\sqrt{2x-6}}{7+\sqrt{2x-6}}\right)\\
&\frac{x+3}{7-\sqrt{2x-6}}=\frac{\left(x+3\right)\left(7+\sqrt{2x-6}\right)}{49-2x-6}\\
&\frac{x+3}{7-\sqrt{2x-6}}=\frac{(x+3)(7+\sqrt{2x-6})}{43-2x}\end{align}
Ejemplo 6. Racionalizando y simplificando. Racionalizar las expresiones
$$a)\ \frac{x^2-16}{\sqrt x-2}\ \ \ \ \ \ \ \ \ \ \ \ b)\frac{4-x^2}{4-\sqrt{x^2+12}}$$
Solución: se multiplica numerador y denominador por el conjugado del denominador (un uno acomodado).
Parte \(a\):
\begin{align}
&\frac{x^2-16}{\sqrt x-2}= \frac{x^2-16}{\sqrt x-2}\left(\frac{\sqrt x+2}{\sqrt x+2}\right)\\
&\frac{x^2-16}{\sqrt x-2}=\frac{\left(x^2-16\right)\left(\sqrt x+2\right)}{x-4}\\
&\frac{x^2-16}{\sqrt x-2}=\frac{\left(x+4\right)\left(x-4\right)\left(\sqrt x+2\right)}{x-4}\\
&\frac{x^2-16}{\sqrt x-2}=\left(x+4\right)\left(\sqrt x+2\right)\\
&b)\ \frac{4-x^2}{4-\sqrt{x^2+12}}=\frac{4-x^2}{4-\sqrt{x^2+12}}\left(\frac{4+\sqrt{x^2+12}} {4+\sqrt{x^2+12}}\right)\\
&\frac{4-x^2}{4-\sqrt{x^2+12}}=\frac{\left(4-x^2\right)\left(4+\sqrt{x^2+12}\right)}{16-\left(x^2+12\right)}\\
&\frac{4-x^2}{4-\sqrt{x^2+12}}=\frac{\left(4-x^2\right)\left(4+\sqrt{x^2+12}\right)}{4-x^2}\\
&\frac{4-x^2}{4-\sqrt{x^2+12}}=4+\sqrt{x^2+12}\end{align}
Ejemplo 7. Racionalizando un numerador. Racionalizar el numerador de la expresión,
$$\frac{\sqrt{x^2+16}-5}{x-3}$$
Solución: multiplicar numerador y denominador por el conjugado del numerador, realizar operaciones planteadas y simplificar hasta el mínimo.
\begin{align}
&\frac{\sqrt{x^2+16}-5}{x-3}=\frac{\sqrt{x^2+16}-5}{x-3}\left(\frac{\sqrt{x^2+16}+5}{\sqrt{x^2+16}+5}\right)\\
&\frac{\sqrt{x^2+16}-5}{x-3}=\frac{x^2+16-25}{\left(x-3\right)\left(\sqrt{x^2+16}+5\right)}\\
&\frac{\sqrt{x^2+16}-5}{x-3}=\frac{x^2-9}{\left(x-3\right)\left(\sqrt{x^2+16}+5\right)}\end{align}
Ejemplo 8. Para finalizar este apartado se presenta un ejemplo avanzado para así afianzar más los conocimientos. Racionalizar las expresiones,
$$a)\frac{x^2-4}{\sqrt[3]{x^2+4}-2}\ \ \ \ \ b)\frac{x-3}{\sqrt[4]{27x}-3}$$
Solución: comience por reescribir las cantidades sub radicales en forma de potencias como,
$$\sqrt[3]{x^2+4}={(x^2+4)}^{1/3}~~ {\rm y}~~ \sqrt[4]{27x}={(27x)}^{1/4}$$ de donde
$$a)\frac{x^2-4}{{(x^2+4)}^{1/3}-2}\ \ \ \ \ \ \ \ \ \ \ b)\frac{x-3}{{(27x)}^{1/4}-3}$$
Parte \(a:\) de \(w^3-x^3=\left(w-x\right)\left(w^2+wx+x^2\right)\) se tiene la forma para racionalizar como sigue.
\begin{align}
&\frac{x^2-4}{{(x^2+4)}^{1/3}-2}=\frac{x^2-4}{{(x^2+4)}^{1/3}-2}\left(\frac{{(x^2+4)}^{2/3}+2{(x^2+4)}^{1/3}+2^2}{{(x^2+4)}^{2/3}+2{(x^2+4)}^{1/3}+2^2}\right)\\
&\frac{x^2-4}{\sqrt[3]{x^2+4}-2}=\frac{\left(x^2-4\right)\left({(x^2+4)}^{2/3}+2{(x^2+4)}^{1/3}+4\right)}{x^2+4-8}\\
&\frac{x^2-4}{\sqrt[3]{x^2+4}-2}=\frac{\left(x^2-4\right)\left({(x^2+4)}^{2/3}+2{(x^2+4)}^{1/3}+4\right)}{x^2-4}\\
&\frac{x^2-4}{\sqrt[3]{x^2+4}-2}={(x^2+4)}^{2/3}+2{(x^2+4)}^{1/3}+4\end{align}
que escrita en forma de radicales es,
$$\frac{x^2-4}{\sqrt[3]{x^2+4}-2}=\sqrt[3]{{(x^2+4)}^2}+2\sqrt[3]{x^2+4}+4$$
Solución \(b\): de \(w^4-x^4=\left(w-x\right)\left(w^3+w^2x+wx^2+x^3\right)\) se tiene la forma para racionalizar.
\begin{align}
&\frac{x-3}{{(27x)}^{1/4}-3}=\frac{x-3}{{(27x)}^{1/4}-3}\left(\frac{\left(27x\right)^\frac{3}{4}+\left(27x\right)^\frac{2}{4}\left(3\right)+\left(27x\right)^\frac{1}{4}\left(3\right)^2+3^3}{\left(27x\right)^\frac{3}{4}+\left(27x\right)^\frac{2}{4}\left(3\right)+\left(27x\right)^\frac{1}{4}\left(3\right)^2+3^3}\right)\\
&\frac{x-3}{{(27x)}^{1/4}-3}=\frac{\left(x-3\right)\left(\left(27x\right)^\frac{3}{4}+3\left(27x\right)^\frac{2}{4}+9\left(27x\right)^\frac{1}{4}+27\right)}{27x-3^4}\\
&\frac{x-3}{{(27x)}^{1/4}-3}=\frac{\left(x-3\right)\left(\left(27x\right)^\frac{3}{4}+3\left(27x\right)^\frac{2}{4}+9\left(27x\right)^\frac{1}{4}+27\right)}{27(x-3)}\\
&\frac{x-3}{{(27x)}^{1/4}-3}=\left(27x\right)^\frac{3}{4}+3\left(27x\right)^\frac{1}{2}+9\left(27x\right)^\frac{1}{4}+27\end{align}
que escrito en forma de radicales es,
\begin{align}
&\frac{x-3}{{(27x)}^{1/4}-3}=\sqrt[4]{{(27x)}^3}+3\sqrt{27x}+9\sqrt[4]{27x}+27\end{align}
