División algebraica.
La división algebraica es una operación que consiste en dadas dos expresiones algebraicas llamadas dividendo y divisor, obtener una tercera cantidad llamada cociente. Al igual que en aritmética puede ser exacta (residuo cero) o entera (residuo distinto de cero).
Algoritmo de la división.
Sean \(P\left(x\right)\) y \(d\left(x\right)\) dos polinomios cualquieras donde \(d\left(x\right)\neq0\) de modo que la divisíón entre ellos está definida, entonces existen los polinomios únicos cociente \(q\left(x\right)\) y residuo \(r\left(x\right)\) tales que:
$$\frac{P\left(x\right)}{d\left(x\right)} \Longrightarrow q\left(x\right)\cdot d\left(x\right)+r\left(x\right)=P\left(x\right)$$
Cociente por divisior, más residuo es igual dividendo, el cual es cococido como el algoritmo de la división y también puede escribirse como:
$$\frac{P\left(x\right)}{d\left(x\right)}=q\left(x\right)+\frac{r\left(x\right)}{d\left(x\right)}$$
Para dividir expresiones algebraicas conviene recordar:
1.Regla de los signos.
\begin{align}
&1.\left(+\right)\div\left(+\right)=+~~~~~~2.\left(-\right)\div\left(-\right)=+\\
&3.\left(+\right)\div\left(-\right)=-~~~~~~4.\left(-\right)\div\left(+\right)=-\end{align}
2. Las leyes de los exponentes, las cuales ya han sido estudiadas con anterioridad y pueden verse en el apartado de potenciación.
Al combinar estos resultados (regla de los signos y leyes de los exponentes) se obtienen las reglas para la división algebraica las cuales pueden verse en las pestañas de más arriba división de monomios y división de polinomios.
Caso 1. División de monomios.
En sentido estricto un monomio es un polinomio de grado uno, sin embargo, para facilitar el aprendizaje en la división se referirá a la división de monomios como un caso particular de la división de polinomios.
Regla de la división de monomios.
1. Dividir signos.
2. Dividir coeficientes.
3. Escribir la parte literal (las letras).
4. Restar los exponentes para cada letra de las bases por separado.
Ejemplo 1. Coeficientes enteros. Determinar el cociente $$C=\frac{6w^2}{-2w}$$ Solución: aplicando la regla anterior, $$C=\frac{+6w^2}{-2w}=-3w^{2-1}=-3w$$ Ejemplo 2. Coeficientes enteros. Determinar el cociente $$C=\frac{-16w^2}{2w^2}$$ Solución: aplicando la regla de los cuatro pasos. \begin{align} &C=\frac{-16w^2}{+2w^2}=-8w^{2-2}\\ &C=-8w^0=-8\left(1\right)=-8\end{align} Ejemplo 3. Coeficientes enteros. Determinar el cociente $$C=\frac{20u^5}{-4u^2}$$ Solución: aplicando los cuatro pasos, $$C=\frac{+20u^5}{-4u^2}=-5u^{5-2}=-5u^3$$ Ejemplo 4. Exponentes literales. Determinar el cociente $$ C=\frac{100u^{2x+4}}{20u^{x-3}}$$ Solución: aplicando la regla de los cuatro pasos, $$C=5u^{2x+4-x+3}=5u^{x+7}$$ Ejemplo 5. Exponentes literales. Determinar el cociente $$C=\frac{7w^{6a+3}x^{4a+2}}{21w^{3a-2}x^{a+2}}$$ Solución: se aplica la regla de los cuatro pasos. $$C=\frac{1}{3}w^{6a+3-3a+2}x^{4a+2-a-2}=\frac{1}{3}w^{3a+5}x^{3a}$$ Ejemplo 6. Coeficientes fraccionarios. Determinar el cociente $$C=\frac{\frac{7}{21}w^5x^4}{\frac{14}{3}w^3x^4}$$ Solución: aplicando la llamada "regla de la herradura u oreja" (el producto de los extremos sobre el producto de los internos) se tiene, $$C=\frac{7(3)}{21(14)}w^2=\frac{1}{14}w^2$$ Ejemplo 7. Aplicación en operaciones con notación científica. Determinar la masa de una partícula sometida a una fuerza neta \(F=12.0\cdot{10^5}N\) si está sometida a una aceleración \(a=3.00\times{10^3}m/s^2\).
Solución: \(F=ma\Longrightarrow m=F/a\) de donde se tiene: $$m=\frac{12.0\cdot10^5\frac{\mathrm{kg}\cdot m}{s^2}}{3.00\cdot10^3\frac{m}{s^2}}=\frac{12.0}{3.00}\times10^{5-3}kg=4.00\times10^2\mathrm{kg}$$
Para más contenidos y luego clic en la pestaña del contenido deseado.
Caso 2. División de un polinomio entre un monomio.
Regla: dividir cada uno de los términos del polinomio entre el monomio, usando la regla de la división de monomios (dividir signos, dividir coeficiente, escribir letras, restar exponentes).
Ejemplo 1. Dividir \(6u^4+10u^5\) entre \(2u^2\)
$$\frac{6u^4+10u^5}{2u^2}=\frac{6u^4}{2u^2}+\frac{10u^5}{2u^2}=3u^2+5u^3$$
Ejemplo 2. Dividir \(12x^5+20x^4-8x^3\) entre \(4x^2\). $$\frac{12x^5+20x^4-8x^3}{4x^2}=\frac{12x^5}{4x^2}+\frac{20x^4}{4x^2}-\frac{8x^3}{4x^2}=3x^3+5x^2-2x$$
Ejemplo 3. Dividir \(20w^4x^2-10w^6x^8y^4\) entre \(5w^2x^2\). $$\frac{20w^4x^2}{5w^2x^2}-\frac{10w^6x^8y^4}{5w^2x^2}=4w^2-2w^4x^6y^4$$
Para más contenidos y luego clic en la pestaña del contenido deseado.
Caso 3. División de polinomio entre polinomio
Para dividir dos polinomios se realizan los siguientes pasos:
1. Ordenar ambos polinomios en forma estándar (de manera descendente) con respecto a la misma letra. Observando si el dividendo está completo o no, si no lo está, completar con ceros o dejar el espacio para los términos de los grados faltantes.
2. Dividir el primer término del dividendo entre el primer término del divisor, usando la regla de la división de monomios.
3. Multiplicar el cociente encontrado por el divisor y sumar el inverso aditivo (cambiarle el signo) del producto al dividendo.
4. Simplificar términos semejantes para determinar el residuo.
5. Agregar el siguiente término del dividendo al residuo encontrado y repetir los pasos anteriores (desde el paso 2) hasta que el dividendo sea de grado menor que el divisor.
Ejemplo 1. Dividir \(2u+6u^2+4u^4-8\) entre \(-2+2u\).
Comience escribiendo los polinomios ordenados y completo (para el dividendo) como \(4u^4+0u^3+6u^2+2u-8\) y \(2u-2\) para el divisor, luego realice cada paso de la regla.

Por el algoritmo de la división cociente por divisor más residuo es igual al dividendo, se comprueba que:
\(\left(2u^3+2u^2+5u+6\right)\left(2u-2\right)+4=4u^4+6u^2+2u-8\).
Ejemplo 2. Dividir \(2x^5+5x^4+10x^3+37x^2+60\) entre \(x^2+5\).
Solución: observando los polinomios se ve que ya estan ordenados, pero el dividendo no está completo, así que esto es lo primero que debe hacer, completar escribiendo \(2x^5+5x^4+10x^3+37x^2+0x+60\) y ahora realizar antes de realizar las operaciones.
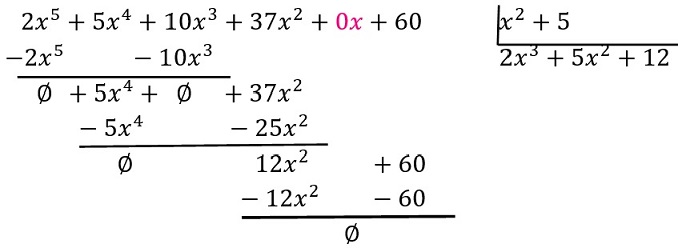
Ejemplo 3. Dividir \(-9n^3+6nm^3+4m^5-6m^2n^2\) entre \(3n+2m^2\).
Solución: comience por ordenar los polinomios en forma estándar con respecto \(m\), completando con ceros los términos faltantes en el dividendo \(\Longrightarrow 4m^5+0m^4+6m^3n-6m^2n^2-9n^3\), luego realice los demás pasos.
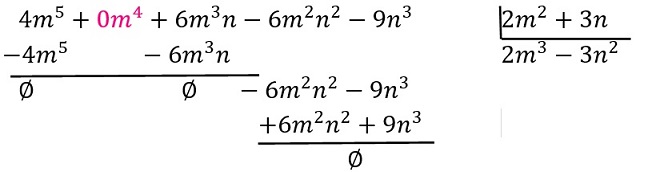
Del algortimo se tiene \(P\left(x\right)=q\left(x\right)\cdot d\left(x\right)+r\left(x\right)\) entonces \(\left(2m^3-3n^2\right)\left(2m^2+3n\right)=4m^5+6m^3n-6m^2n^2-9n^3\).
Ejemplo 4. Dividir \(x^{12}-64\) entre \(x^2-2\).
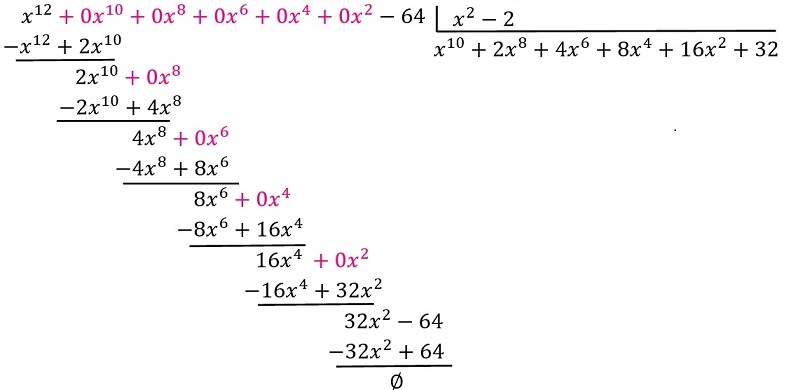
Luego se tiene,
\(\left(x^{10}+2x^8+4x^6+8x^4+16x^2+32\right)\left(x^2-2\right)=x^{12}-64\)
