Multiplicación de polinomios.
La multiplicación algebraica es la operación que consiste en, dadas dos o más cantidades llamadas factores determinar otra cantidad llamada producto.
Antes de multiplicar algebraicamente conviene recordar las propiedades de los exponentes (ya han sido estudiadas) y la multiplicación de los signos.
\begin{array}i
1.~~\left(+\right)\left(+\right)=+&\ \ \ \ 2.~~\left(-\right)\left(-\right)=+&\ \ \ \ 3.~~ \left(+\right)\left(-\right)=-\ \ \ \ &4. \left(-\right)\left(+\right)=-\end{array}
De la propiedad distributiva de la multiplicación para la adición y la diferencia se tiene lo siguiente:
\(1.~~\textcolor{#ff0080}{a}\left(m+n-w-h+\cdots\right)=\textcolor{#ff0080}{a}m+\textcolor{#ff0080}{a}n-\textcolor{#ff0080}{a}w-\textcolor{#ff0080}{a}h+\cdots\)
\begin{align}
2.~~\left(\textcolor{#ff0080}{a}+\textcolor{#ff0080}{b}+\textcolor{#ff0080}{c}+\cdots\right)\left(m+n+\cdots\right)
&=\textcolor{#ff0080}{a}\left(m+n+\cdots\right)+\textcolor{#ff0080}{b}\left(m+n\cdots\right)\\
&+\textcolor{#ff0080}{c}\left(m+n\cdots\right)+\cdots
\end{align}
Al combinar los resultados anteriores se obtienen las reglas para realizar la multiplicación algebraica, las cuales se presentan en las pestañas de arriba.
Caso 1. Producto de monomios.
Regla general para multiplicar dos o más monomios.
1. Multiplicar signos.
2. Multiplicar coeficientes.
3. Escribir la parte literal (las letras).
4. Sumar los exponentes para cada letra por separado.
Producto de monomios con coeficientes enteros.
Ejemplo 1. Multiplicar \(4\left(5x\right)\Longrightarrow4\left(5x\right)=20x\)
Ejemplo 2. Multiplicar \(-4\left(5x\right)\Longrightarrow-4\left(5x\right)=-20x\)
Ejemplo 3. Multiplicar \(4\left(-5x\right)\Longrightarrow4\left(-5x\right)=-20x\)
Ejemplo 4. Multiplicar \(2w\left(4w^2\right)\Longrightarrow2\left(4\right)w^{1+2}=8w^3\)
Ejemplo 5. Multiplicar \(4mn\left(6m^2n\right)\Longrightarrow4\left(6\right)m^{1+2}n^{1+1}=24m^3n^2~~~~~~~~~~~~~~\)
Ejemplo 6. Multiplicar \(-4w^3x^3\left(-8w^3x^4\right)\Longrightarrow-4\left(-8\right)w^{3+3}x^{3+4}=32w^6x^7\)
Ejemplo 7. Multiplicar \(12hk\left(-6h^2k^3\right)\Longrightarrow12\left(-6\right)h^{1+2}k^{1+3}=-72h^3k^4\)
Ejemplo 8. Coeficientes fraccionarios. Realizar el producto de $$\left(\frac{3}{2}wx\right)\left(-\frac{4}{5}wx^2\right)=-\frac{3\cdot4}{2\cdot5}w^{1+1}x^{1+2}=-\frac{6}{5}w^2x^3$$ Ejemplo 9. Coeficientes fraccionarios. Realizar el producto de $$\left(-\frac{4}{3}u\right)\left(\frac{3}{8}u^3\right)=\ -\frac{4\cdot3}{3\cdot8}u^{1+3}=-\frac{1}{2}u^4$$ Ejemplo 10. Exponentes literales. Realizar el producto de $$\left(\frac{4}{5}u^{2x+1}\right)\left(\frac{3}{8}u^{x-3}\right)=\ \frac{4\cdot3}{5\cdot8}u^{2x+1+x-3}=\frac{3}{10}u^{3x-2}$$
Ejemplo 11. Notación científica. De la segunda ley de Newton se sabe que si la masa de un cuerpo es constate, entonces la magnitud de fuerza neta ejercida sobre ella está dada por \(F=ma\) (medida en newton (N) en el S.I.). Determinar la magnitud de la fuerza ejercida sobre un electrón cuya aceleración es \(a=3.00\times{10}^3m/s^2\)
Solución: \(F=ma\) donde la masa del electrón es \(9.11\cdot{10}^{-31}\ {\rm kg}\)
\begin{align}
&F=\left(9.11\times{10}^{-31} {\rm kg}\right)\left(3.00\times{10}^3m/s^2\right)\\
&F=27.33\times{10}^{-28} {\rm N}\end{align}
De donde tomando en cuenta las cifras significativas se tiene:
$$F=2.73\times{10}^{-27}{\rm N}$$
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Caso 1. Producto de monomios.
Regla general para multiplicar dos o más monomios.
1. Multiplicar signos.
2. Multiplicar coeficientes.
3. Escribir la parte literal (las letras).
4. Sumar los exponentes para cada letra por separado.
Producto de monomios con coeficientes enteros.
Ejemplo 1. Multiplicar \(4\left(5x\right)\Longrightarrow4\left(5x\right)=20x\)
Ejemplo 2. Multiplicar \(-4\left(5x\right)\Longrightarrow-4\left(5x\right)=-20x\)
Ejemplo 3. Multiplicar \(4\left(-5x\right)\Longrightarrow4\left(-5x\right)=-20x\)
Ejemplo 4. Multiplicar \(2w\left(4w^2\right)\Longrightarrow2\left(4\right)w^{1+2}=8w^3\)
Ejemplo 5. Multiplicar \(4mn\left(6m^2n\right)\Longrightarrow4\left(6\right)m^{1+2}n^{1+1}=24m^3n^2~~~~~~~~~~~~~~\)
Ejemplo 6. Multiplicar \(-4w^3x^3\left(-8w^3x^4\right)\Longrightarrow-4\left(-8\right)w^{3+3}x^{3+4}=32w^6x^7\)
Ejemplo 7. Multiplicar \(12hk\left(-6h^2k^3\right)\Longrightarrow12\left(-6\right)h^{1+2}k^{1+3}=-72h^3k^4\)
Ejemplo 8. Coeficientes fraccionarios. Realizar el producto de $$\left(\frac{3}{2}wx\right)\left(-\frac{4}{5}wx^2\right)=-\frac{3\cdot4}{2\cdot5}w^{1+1}x^{1+2}=-\frac{6}{5}w^2x^3$$ Ejemplo 9. Coeficientes fraccionarios. Realizar el producto de $$\left(-\frac{4}{3}u\right)\left(\frac{3}{8}u^3\right)=\ -\frac{4\cdot3}{3\cdot8}u^{1+3}=-\frac{1}{2}u^4$$ Ejemplo 10. Exponentes literales. Realizar el producto de $$\left(\frac{4}{5}u^{2x+1}\right)\left(\frac{3}{8}u^{x-3}\right)=\ \frac{4\cdot3}{5\cdot8}u^{2x+1+x-3}=\frac{3}{10}u^{3x-2}$$
Ejemplo 11. Notación científica. De la segunda ley de Newton se sabe que si la masa de un cuerpo es constate, entonces la magnitud de fuerza neta ejercida sobre ella está dada por \(F=ma\) (medida en newton (N) en el S.I.). Determinar la magnitud de la fuerza ejercida sobre un electrón cuya aceleración es \(a=3.00\times{10}^3m/s^2\)
Solución: \(F=ma\) donde la masa del electrón es \(9.11\cdot{10}^{-31}\ {\rm kg}\)
\begin{align}
&F=\left(9.11\times{10}^{-31} {\rm kg}\right)\left(3.00\times{10}^3m/s^2\right)\\
&F=27.33\times{10}^{-28} {\rm N}\end{align}
De donde tomando en cuenta las cifras significativas se tiene:
$$F=2.73\times{10}^{-27}{\rm N}$$
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Caso 2. Producto de polinomios de más de dos términos.
Regla general del producto de polinomios.
1. Aplicar la propiedad distributiva.
2. Multiplicar con la regla de la multiplicación de monomios.
3. Simplificar y ordenar en forma estándar.
Productos con coeficientes enteros.
Ejemplo 1. Monomio por binomio. Multiplicar \(6x\left(2w+5x\right)\).
Solución: aplicando la propiedad distributiva \(\textcolor{#ff0080}{a}(m+n)=\textcolor{#ff0080}{a}m+\textcolor{#ff0080}{a}n\) se tiene,
\(6x\left(2w+5x\right)=6x\left(2w\right)+6x\left(5x\right)\)
\(6x\left(2w+5x\right)=12wx+30x^2\)
Ejemplo 2. Monomio por trinomio. Multiplicar \(2m^2\left(3m-4mn+n\right)\).
Solución: aplicando \(\textcolor{#ff0080}{a}(m+n+u)=\textcolor{#ff0080}{a}m+\textcolor{#ff0080}{a}n+\textcolor{#ff0080}{a}u\) se tiene,
\begin{align}
&2m^2\left(3m-4mn+n\right)=2m^2\left(3m\right)-2m^2\left(4mn\right)+2m^2n\\
&2m^2\left(3m-4mn+n\right)=6m^3-8m^3n+2m^2n\end{align}
Ejemplo 3. Producto de dos binomios. Multiplicar \(\left(2+x\right)\left(x+3\right)\)
Soluión: aplicando la propiedad distributiva en la forma \((\textcolor{#ff0080}{a}+\textcolor{#ff0080}{b})(m+n)=\textcolor{#ff0080}{a}(m+n)+\textcolor{#ff0080}{b}(m+n)\) se tiene,
\begin{align}
&\left(2+x\right)\left(x+3\right)=2\left(x+3\right)+x\left(x+3\right)\\
&\left(2+x\right)\left(x+3\right)=2x+6+x^2+3x\\
&\left(2+x\right)\left(x+3\right)=x^2+5x+6\end{align}
Ordenando y simplificando.
Ejemplo 4. Producto de dos binomios.
Multiplicar \(\left(2w-n\right)\left(w+2n\right)\)
Soluión: aplicando \((\textcolor{#ff0080}{a}+\textcolor{#ff0080}{b})(m+n)=\textcolor{#ff0080}{a}(m+n)+\textcolor{#ff0080}{b}(m+n)\) se tiene,
\(\left(2w-n\right)\left(w+2n\right)=2w\left(w+2n\right)-n\left(w+2n\right)\) Propiedad distributiva.
\(\left(2w-n\right)\left(w+2n\right)=2w^2+4nw-nw-2n^2\) Multiplicando.
\(\left(2w-n\right)\left(w+2n\right)=2w^2+3nw-2n^2\) Ordenando y simplificando.
Ejemplo 5. Cuadrado de un binomio. Determinar \(\left(u+v\right)^2\)
Solución: desarrollando potencia y aplicando la propiedad distributiva, se tiene,
\begin{align}
&(u+v)^2=
(\textcolor{#ff0080}{u}+\textcolor{#ff0080}{v})(u+v)\\
&(u+v)^2=\textcolor{#ff0080}{u}(u+v)+\textcolor{#ff0080}{v}(u+v)\\
&(u+v)^2=u^2+uv+uv+v^2\\
&(u+v)^2=u^2+2uv+v^2\end{align}
Ordenando y simplificando.
Ejemplo 6. Binomios conjugados. Multiplicar \(\left(2x+3\right)\left(2x-3\right)\)
Solución:
\(\left(2x+3\right)\left(2x-3\right)=2x\left(2x-3\right)+3\left(2x-3\right)\) por la propiedad distributiva.
\(\left(2x+3\right)\left(2x-3\right)=4x^2-6x+6x-9\) Multiplicando.
\(\left(2x+3\right)\left(2x-3\right)=4x^2-9\) Simplificando.
Note lo que pasa al multiplicar un binomio conjugado de la forma \((u+v)(u-v)\) o \((u-v)(u+v),\) el resultado simpre será \(u^2-v^2\) y listo.
Ejemplo 7. Coeficientes fraccioanarios. Determinar el producto de multiplicar $$\left(\frac{2}{3}u-3\right)\left(u+\frac{3}{5}\right)$$ Solución: sea \(p\) el producto buscado, entonces se tiene, \begin{align} &p=\frac{2}{3}u\left(u+\frac{3}{5}\right)-3\left(u+\frac{3}{5}\right)\\ &p=\frac{2\cdot1}{3}u^2+\frac{2\cdot3}{3\cdot5}u-3u-\frac{3\cdot3}{5}\\ &p=\frac{2}{3}u^2+\frac{2}{5}u-3u-\frac{9}{5}\\ &p=\frac{2}{3}u^2+\frac{5(-3)+2}{5}u-\frac{9}{5}\\ &p=\frac{2}{3}u^2-\frac{13}{5}u-\frac{9}{5}\end{align} Ejemplo 8. Coeficientes fraccioanarios. Determinar el producto de $$\left(\frac{4}{9}h-4k\right)\left(\frac{1}{3}h+\frac{3}{4}k\right)$$ Solución: sea \(p\) el producto buscado, de la propiedad distributiva y la regla de la multiplicación de monomios se tiene, \begin{align} &p=\frac{4}{9}h\left(\frac{1}{3}h+\frac{3}{4}k\right)-4k\left(\frac{1}{3}h+\frac{3}{4}k\right)\\ &p=\frac{4\cdot1}{9\cdot3}h^2+\frac{4\cdot3}{9\cdot4}hk-\frac{4\cdot1}{3}hk-\frac{4\cdot3}{4}k^2\\ &p=\frac{4\cdot1}{9\cdot3}h^2+\frac{1}{3}hk-\frac{4}{3}hk-\frac{4\cdot3}{4}k^2\\ &p=\frac{4}{27}h^2-hk-3k^2\end{align}
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Una señal de tránsito tiene forma de triángulo rectángulo. Si las longitudes de los lados perpendiculares están dadas por \(l_1=2u+3\) y \(l_2=5u+4\).
a. Determinar la medida de la superficie.
b. Determinar la medida del lado mayor en términos de \(u.\)
Determinar el área total y el volumen de una caja prismática sin tapa, cuyas aristas están dadas por \(a=2u-4\).
Cierto diseñador industrial de una compañía, debe diseñal una nueva lata para uno de sus productos. Si la lata debe tener forma de un cilindro circular recto y el radio de la base es \(r=2u+2\) y su altura \(h=6u+4\).
a. Realiza un boceto de la lata.
b. Determina el volumen de la lata.
c. Determina en términos de \(u\) la cantidad total de material que se debe usar para la construcción de la lata (medida de la superficie).
Dos terrenos tienen dimensiones como se muestra en la figura, acerca de ellos se pide:
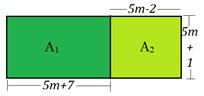
1. Determinar la medida de la superficie de \(A_1\) y \(A_2\).
2. Determinar el área total que ocupan los terrenos.
3. Determinar la medida del contorno total y de cada uno de los terrenos.
4. Cuanto mayor es el área \(A_1\) con respecto del área \(A_2\).
Volumen de una esfera. Determinar el volumen de una pelota de baloncesto cuyo radio está dado por la expresión \(r=3u-6\).
Determinar el producto de: $$\left(\frac{2x^2}{5}+\frac{10}{3}\right)\left(\frac{2x^2}{5}-\frac{10}{3}\right)$$
Volumen de un prisma rectangular. Determinar el volumen de una piscina con forma de prisma rectangular, cuyas aristas miden \(4u+5, 8u+4~ y~ 4u+6\).
Área de un trapecio. Un terreno tiene forma trapezoidal tal que, su base mayor mide \(6u-4\), su base menor mide \(4u-8\) y su altura es \(3u+10\). Determinar la medida de su superficie.
