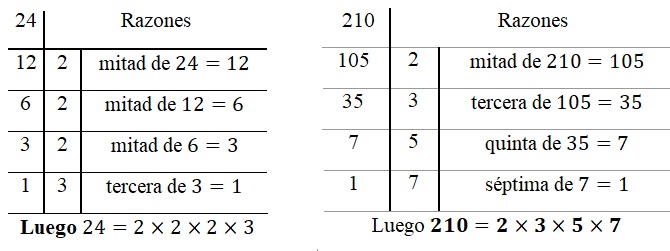Descomposición factorial prima.
La descomposición factorial o factorización prima de un número es un procedimiento que consiste en descomponer un número en sus factores primos.
Factorizar un número en factores primos, es encontrar todos los factores primos de dicho número. Por ejemplo, puede escribir el número 24 como \(24=2\times2\times2\times3\) de modo que el dos y el tres, son factores primos del 24.
Para determinar los factores primos de un número se aplican los criterios de divisibilidad una y otra vez, cuantas veces sea necesario, siguiendo el orden de los números primos preferiblemente. Es decir, como el primer número primo es el dos, el primer criterio que debe aplicar es el de divisibilidad por dos, luego por tres, por cinco, por siete y así sucesivamente.
Ejemplo 1 Determinar todos los factores primos de los números \(24\) y \(210\).
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Máximo común divisor.
El máximo común divisor (m.c.d.) de dos o más números, es el mayor número que los divide. Para determinar el m.c.d. de dos o más números, se determinan los factores primos comunes a los números y el m.c.d. es el producto de los factores primos comunes.


Números coprimos
Si el m.c.d. de dos o más números es el número uno, se dice que dichos números son primos entres sí o coprimos, por ejemplo 3, 7 y 11 son coprimos porque su m.c.d. es uno.
Ejemplo 3. Aplicación del m.c.d. Se tienen dos trozos de cuerdas, el menor de 80 pies y el mayor de 100 pies. Si se desea cortar ambas cuerdas en pedazos de igual longitud. Determinar la mayor longitud que pueden tener los pedazos. ¿Cuántos pedazos se pueden tener?
Puede dividir las cuerdas en pedazos de longitud igual a 20ft, ya que el m. c. d. de 80 y 100 es 20 (compruebe esto), luego se tienen 9 pedazos de 20ft cada uno.
Note que en este caso el m.c.d no es el \(27\) sino \(9\), esto es poque \(27\), \(63\) y \(99\) son múltiplos de \(9\).
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Mínimo común múltiplo (m.c.m.).
El mínimo común múltiplo (m.c.m.) de dos o más números es el menor múltiplo común a todos ellos.
Para determinar el mínimo común múltiplo de dos o más números, el método más fácil es el de la “parrilla”, en él se descomponen los números en sus factores primos, en una misma “parrilla” hasta que los números de la última fila sean todos uno (exceptuando la columna de los factores primos), luego el m.c.m. es el producto de los factores primos encontrados.
Ejemplo: Determinar el mínimo común múltiplo de 12 y 72.
Solución: escriba los números en una misma “parrilla” y realice la descomposición factorial.

Ejemplo. Aplicación del m. c. m. En una agrupación musical A toca a cuatro pulsos, B toca a ocho pulsos, C toca a doce pulsos y D a dieciséis pulsos. Si todos los músicos empiezan a tocar al mismo tiempo, determinar en cuántos pulsos sus periodos volverán a iniciar al mismo tiempo otra vez.
Solución: los músicos volverán a iniciar al mismo tiempo cuando los pulsos se encuentren de nuevo, por lo cual se debe determinar el mínimo común múltiplo de los pulsos, el m.c.m. de 4, 8, 12 y 16 es 48. Luego en 48 pulsos los músicos volverán a iniciar nuevamente todos juntos.
Ejemplo de aplicación del m. c. m. En una calle de cierta ciudad hay tres semáforos consecutivos, A, B y C correspondientes a tres intersecciones. Si los tres semáforos se ponen en funcionamiento en el mismo instante todos en verde, y el periodo (tiempo en que tarda en volver a verde) para cada uno de ellos es, cincuenta segundos para A, ochenta segundos para B y sesenta segundos para C. Determinar en cuánto tiempo los semáforos volverán a estar en verde al mismo tiempo.
Solución: los semáforos volverán a estar en verde al mismo tiempo, cuando sus periodos vuelvan a coincidir. Esto ocurre en el mínimo común múltiplo de los tiempos de sus periodos.