Vectores, conceptos básicos.
El término vector es empleado en ciencia y matemática para denotar una cantidad la cual tiene magnitud (tamaño) y dirección. Algunas cantidades físicas como el desplazamiento, las velocidades, las fuerzas, ente otras son de naturaleza vectoriales (necesitan para quedar bien especificada que se exprese su tamaño y dirección). Si se pide que una persona realice una fuerza para mover un mueble ¿Hacia dónde debe la persona dirigir su esfuerzo físico? Piense en que se quería mover el mueble hacia la derecha y la persona dirigió su fuerza hacia la izquierda. ¿Se obtendrá el resultado esperado?
Un vector es un ente matemático que tiene módulo (magnitud) y dirección, descripto geométricamente con una semirecta o rayo (flecha de un solo sentido). El módulo representa “el cuánto” que tan grande o pequeño es el vector, la dirección es el menor ángulo medido al eje \(x\) positivo en sentido contrario a las agujas del reloj (si es en el plano) y si es en el espacio a través de los ángulos que forma el vector con los vectores canónicos (se estudian más adelante).
Representación de vectores.
La primera representación de vectores es como un segmento de recta dirigido desde un punto \(P\) hasta un punto \(Q.\) donde \(P\) es el punto inicial (cola) y \(Q\) es el punto final (punta). Así en la figura de la izquierda el vector \( \vec{PQ}\neq\vec{QP}\) ya que tienen igual dirección (ángulo medido al eje \(x\) positivo), pero sentido opuesto.
Representación gráfica de vectores.
En cuanto a la representación gráfica un vector puede ser en elemento del plano o del espacio. En el caso de que el vector pertenezca al espacio de coordenadas por convención se utilizará el sistema de coordenadas espaciales dextrógiro (sistema derecho) como se muestra en la figura dos.
Oservación importante: Debido a que el mundo físico solo posee tres cordenadas espaciales, el estudio de vectores aquí presentado se centra en el estudio de vectores en el plano (dos dimensiones) y en el espacio (tres dimensiones).
Componentes de un vector.
Es posible representar un vector de distintas formas las más comunes y de uso en ciencias físicas son:
Por una letra en negritas como \(\mathbf{v}\), o por una letra con una flecha en dirección izquierda a derecha sobre ella \(\mathbf{\vec{v}}\), en forma de una matriz renglón (o columna si se desea) por ejemplo, \( \mathbf{u}=\left< u_1,u_2,u_3,\cdots u_n\right>\) donde las cantidades \(u_1,u_2,u_3\cdots u_n\) son llamadas componentes del vector.
En la escritura manuscrita las notación de vectores que predomina por lo general, es la notación con flecha encima (\(\mathbf{\vec{v}}\)) por razones obvias (no es factible escribir en negritas de forma manuscrita cada vez que se está escribiendo un vector).
Sea el punto \(P\left(p_1,p_2\right)\) y sea el punto \(Q\left(q_1,q_2\right)\) en el plano o \(P\left(p_1,p_2,p_3\right)\) y \(Q\left(q_1,q_2,q_3\right)\) si es en el espacio, las coordenadas del vector \(\mathbf{u}\) que va desde \(P\) hacia \(Q\) se representa en función de sus componentes como,
Componentes de un vector \(\mathbf{u}\)
\(\mathbf{\vec{u}}=\left< q_1-p_1,q_2-p_2\right>=\left< u_x,u_y\right>\) para el plano.
\(\mathbf{\vec{u}}=\left< q_1-p_1,q_2-p_2,q_3-p_3\right>=\left< u_x,u_y,u_z\right>\).
Módulo o magnitud de un vector.
Sea \(\mathbf{\vec{u}}=\left< u_x,u_y,u_z\right>\) un vector en el espacio (si es en el plano \(u_z=0\)) entonces el módulo o longitud del vector también llamado longitud o norma por algunos autores se define como la raíz cuadrada de la suma de los cuadrados de sus componentes, esto es
Módulo de un vector
\begin{align} ||\mathbf{\vec{u}}||&=\sqrt{u_x^2+u_y^2}~~~~~~ {\rm para ~el~ plano.}\\ ||\mathbf{\vec{u}}||&=\sqrt{u_x^2+u_y^2+u_z^2}~~~~ {\rm para~ el ~espacio.} \end{align} Ver Ejercicio I Ej.1 en la sección de ejercicios.
Vector nulo o cero.
Se denomina vector cero o vector nulo al vector en el cual todas las componentes son cero y por tal razón su módulo es cero. Si el módulo de un vector es cero, entonces obligatoriamente \(\mathbf{\vec{u}} =\mathbf{\vec{0}}\)
Múltiplo escalar de un vector.
En el contexto de los vectores los números son llamados escalares, así cualquier \(c|c\in\mathbb{C}\) es un escalar, el producto de un escalar \(c\) por un vector \(\mathbf{\vec{u}}\) esta dado por \(c\mathbf{\vec{u}}=\left< cu_x,cu_y,cu_z\right>.\)
Si el módulo de un vector \(\mathbf{\vec{u}}\) se multiplica por un escalar \(c\) (distinto de cero por convención) el resultado es un nuevo vector cuyo modulo es \(c\) veces el módulo del vector \(\mathbf{\vec{u}},\) esto es, y de esto se concluye que,
Módulo de un múltiplo escalar.
$$||c\mathbf{\vec{u}}||=c||\mathbf{\vec{u}}||$$ La demostración a esto es bastante simple, partiendo de \(c\mathbf{\vec{u}}=(cu_x,cu_y,cu_z):\) \begin{align} \left|\left|c\mathbf{\vec{u}}\right|\right|&=\sqrt{\left(cu_x\right)^2+\left(cu_y\right)^2+\left(cu_z\right)^2}\\ \left|\left|c\mathbf{\vec{u}}\right|\right|&=\sqrt{c^2u_x^2+c^2u_y^2+c^2u_z^2}\\ \left|\left|c\mathbf{\vec{u}}\right|\right|&=\sqrt{c^2\left(u_x^2+u_y^2+u_z^2\right)}\\ \left|\left|c\mathbf{\vec{u}}\right|\right|&=c\sqrt{\left(u_x^2+u_y^2+u_z^2\right)}\\ \left|\left|c\mathbf{\vec{u}}\right|\right|&=c\left|\left|\mathbf{\vec{u}}\right|\right| l.q.q.d.\end{align}
Vectores unitarios.
Se dice que un vector unitario \(\mathbf{\vec{u}}\) denotado por \(\hat{\mathbf{u}}\) es un vector tal que el módulo de vector \(\mathbf{\vec{u}}\) es uno, esto es \(||\hat{\mathbf{u}}||=1.\)
Un vector unitario \(\hat{\mathbf{u}}\) en la dirección de otro vector cualquiera \(\mathbf{\vec{v}}\) queda determinado al dividir las componentes del vector \(\mathbf{\vec{v}}\) entre su módulo.
Vector unitario \(\hat{\mathbf{u}}\) en dirección \( \mathbf{\vec{v}}\)
$$\hat{\mathbf{u}}=\frac{\mathbf{\vec{v}}}{||\mathbf{\vec{v}}||}=\frac{\mathbf{1}}{||\mathbf{\vec{v}}||}\mathbf{\vec{v}}$$ Ver los ejemplos Ej2 y Ej3 del apartado Ejercicio I en la pestaña de arriba.
Vectores unitarios canónicos
En términos de las coordenadas espaciales \(x,\ y,z,\) se definen los llamados vectores unitarios canónicos, \(\mathbf{\hat{i}},~\hat{\mathbf{j}},~\hat{\mathbf{k}}\) los cuales se escribiran por acuerdo sin el circunflejo (sombrerito) como siguen:
\begin{align}
&\mathbf{i}=\left< 1,0\right>;~~~~\mathbf{j}=\left< 0,1\right>~~{\rm en~el~plano}\\
&\mathbf{i}=\left< 1,0,0\right>;~~~~ \mathbf{j}=\left< 0,1,0\right>, ~~~~\mathbf{k}=\left< 0,0,1\right>~~{\rm en~el~espacio}\end{align}
La descripción geométrica de los vectores canónicos se muestra en la figura de la izquierda. En función de estos vectores un vector \(\mathbf{\vec{v}}\) se escribe como,
$$\mathbf{\vec{v}}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k}$$
donde \(v_x, v_y\) y \(v_z\) son las componentes del vector.
Si se conoce la dirección \(\phi\) de un vector en el plano \(\mathbf{\vec{v}},\) entonces un vector unitario en la dirección del vector \(\mathbf{\vec{v}}\) es el vector $$\hat{\mathbf{u}}=\cos{\phi}\mathbf{i}+\sin{\phi}\mathbf{j}.$$ Para el caso del espacio la descripción matemática se realiza mediante el uso de los llamados ángulos directores del vector (ángulo entre cada uno de los ejes y el vector). Sea \(\mathbf{\vec{r}}\) un vector de posición cualquiera en el espacio y sean \(\alpha\) (alfa), \(\beta\) (beta) y \(\gamma\) (gamma) los ángulos formados por los vectores unitarios canónicos \(\mathbf{i},~ \mathbf{j},~ \mathbf{k}\) y el vector \(\mathbf{\vec{r}}\), entonces las coordenadas del vector \(\mathbf{\vec{r}}\) están dadas por, $$r_x=r\cos{\alpha};\ \ \ r_y=r\cos{\beta};\ \ \ \ r_z=r\cos{\gamma}$$ y el vector puede escribirse como $$\mathbf{\vec{r}}=r\cos{\alpha}\mathbf{i}+r\cos{\beta}\mathbf{j}+r\cos{\gamma}\mathbf{k}$$ los cosenos de los ángulos directores son llamados cosenos directores, los cuales cumplen la condición de igualdad $$\cos^2{\alpha}+\cos^2{\beta}+\cos^2{\gamma}=1$$ Ver el Ej5 del apartado Ejercicio I de la pestaña superior.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Adición de vectores.
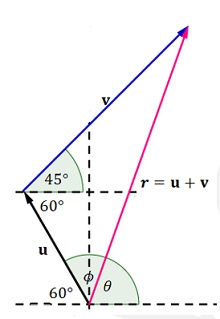
Dados dos vectores no nulos en el plano \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) entonces su adición puede realizarse gráficamente al dibujar los vectores en el plano de modo que el punto inicial de \(\mathbf{\vec{v}}\) coincide con el punto final de \(\mathbf{\vec{u}}\), el vector \(\mathbf{\vec{r}}= \mathbf{\vec{u}}+\mathbf{\vec{u}}\) es el vector cuyo punto inicial coincide con el punto inicial de \(\mathbf{\vec{u}}\), y cuyo punto final coincide con el punto final de \(\mathbf{\vec{v}}\). La magnitud de \(\mathbf{\vec{r}}\) es la longitud de la línea trazada desde \(\mathbf{\vec{u}}\) hasta \(\mathbf{\vec{v}}\) la cual forma un triángulo con los vectores y por esta razón el nombre de método del triángulo como se observa en la figura. Si el dibujo es hecho a escala el valor de \(\mathbf{\vec{r}}\) se obtiene al medir su longitud. De manera analítica los valores se obtienen al aplicar la ley de los cosenos al vector suma, este hecho se muestra en el Ej4 del apartado Ejercicios I.
Aunque este método es funcional y a menudo muy usado en ciencias físicas, para su aplicanción requiere del uso de instrumentos geometricos para dibujo, por lo que suele considerarse un método tedioso y se prefiere hacer énfasis en la adición de vectores a través del método de las componentes.
Adición de vectores por componentes.
Sean los vectores no nulos \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) definidos en el plano o el espacio, entonces el vector resultante \(\mathbf{\vec{r}}=\mathbf{\vec{u}}+\mathbf{\vec{v}}\) está dado por,
Suma vectorial por componentes \(\mathbf{\vec{r}}= \mathbf{\vec{u}}+\mathbf{\vec{v}}\)
\(\mathbf{\vec{r}}=(u_x+v_x)\mathbf{i}+(u_y+v_y)\mathbf{j}\) para el plano.
\(\mathbf{\vec{r}}=(u_x+v_x)\mathbf{i}+(u_y+v_y)\mathbf{j}+(u_z+v_z)\mathbf{k}\) para el espacio.
Para una mayor comprensión ver los ejemplos Ej6, Ej7, Ej8, Ej9, Ej10 del apartado Ejercicios I pestaña superior.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Producto escalar.
Dados dos vectores \(\mathbf{\vec{u}}=\left< u_1,u_2,u_3,⋯,u_n\right>\) y \(\mathbf{\vec{v}}=\left< v_1,v_2,v_3,⋯,v_n\right>\) entonces el producto escalar o producto interno de ellos, también llamado producto punto por su notación \(\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}\) está definido como,
Producto escalar de vectores
$$\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}=u_1v_1+u_2v_2+u_3v_3+\cdots+u_nv_n$$ Recuerde que para sistemas físicos, un vector \(\mathbf{\vec{r}}\) solo solo puede tener como máximo tres componentes, esto es \(\mathbf{\vec{r}}=\left< r_x,r_y,r_z\right>\), con lo cual es posible escribir el producto escalar como, $$\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}=u_1v_1+u_2v_2+u_3v_3=uv\cos{\phi}$$ De manera alternativa es posible escribir el producto escalar como $$\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}=uv\cos{\phi}$$ donde \(u\) y \(v\) son los módulos de los vectores y \(\phi\) es el ángulo comprendido por ellos.
Ver Ej1 del apartado Ejercicios II.
Propiedades del producto escalar.
El producto escalar (por ser un número) hereda algunas de las propiedades directas de la multiplicación como se muestra a continuación.
1. Múltiplo escalar: \(c(\mathbf{\vec{u}}\cdot\mathbf{\vec{v}})=c\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}=\mathbf{\vec{u}}\cdot c\mathbf{\vec{v}}\)
2. Conmutativa: \(\mathbf{\vec{u}}\cdot\mathbf{\vec{v}} =\mathbf{v}\cdot\mathbf{u}\)
3. Distributiva: \(\mathbf{\vec{r}}\cdot(\mathbf{\vec{u}}+\mathbf{\vec{v}})=\mathbf{r}\cdot\mathbf{\vec{u}}+\mathbf{\vec{r}}\cdot\mathbf{\vec{v}}\)
4. Elemento absorbente: \(\mathbf{\vec{0}}\cdot\mathbf{\vec{u}}=\mathbf{\vec{0}} \)
5. Producto escalar consigo mismo: \(\mathbf{\vec{u}}\cdot\mathbf{\vec{u}}=||\mathbf{\vec{u}}||^2\)
Ángulo entre dos vectores.
Existen diversas formas de observar el ángulo entre dos vectores, una de ella es a través de la definición alternativa del producto escalar. Sean los vectores \(\mathbf{u}\) y \(\mathbf{v}\) dos vectores cualquiera no nulos, definidos en el plano o en el espacio y sea \(\theta\) el ángulo entre ellos, entonces,
Ángulo entre dos vectores
$$\cos{\theta}=\frac{\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}}{||\mathbf{\vec{u}}||||\mathbf{\vec{v}}||} ⟹ \theta=\cos^{-1}\frac{\mathbf{\vec{u}}\cdot\mathbf{\vec{v}}}{||\mathbf{\vec{u}}||||\mathbf{\vec{v}}||}$$
La demostración a esto se obtiene de manera directa de la ley de los cosenos, y las propiedades del producto escalar. La figura de izquierda se muestra algunos resultados interesantes del ángulo entre dos vectores. Donde se debe notar que, si el ángulo entre los vectores es cero, son paralelos, si \(\phi=180°\) son llamados antiparalelos. Además, si los vectores \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) son paralelos uno de ellos es múltiplo escalar del otro, esto es \(\mathbf{\vec{u}}=c\mathbf{\vec{v}}=\left< cv_1,cv_2,cv_3\right>.\)
Ejemplo. Verificar en cada caso si los vectores dados son paralelos o no. \begin{align} \mathbf{\vec{u}}&=\left< 2,3,5\right> {\rm ~~y~~} \mathbf{\vec{v}}= \left< 2/3,1,5/3\right>\\ \mathbf{\vec{u}}&=\left< 7,3,0\right> {~~\rm y~~} \mathbf{\vec{v}}=\left< 7,2,1\right>\\ \end{align} Solución: dividiendo cada una de las componentes del vector \(\mathbf{\vec{u}}\) entre tres en el primero de los casos se obtiene el vector \(\mathbf{\vec{v}}\) de donde es posible escribir,\(\mathbf{\vec{u}}=3\mathbf{\vec{v}}\) y por tanto son paralelos. Para el segundo caso se puede concluir que no son paralelos al observar que no existe ningún c\neq0 que al multiplicar \(cv_z=0.\)
Vectores ortogonales
Para el caso en que \(\phi=90°\) se dice que los vectores son ortogonales (perpendiculares).
Definición de vectores ortogonales
El vector \(\mathbf{u}\) es ortogonal a \(\mathbf{v}\) si y solo si \(\mathbf{u}\cdot\mathbf{v}=0\)
Se ha de notar que para los vectores unitarios canónicos \(\mathbf{i}=\left< 1,0,0\right>;\mathbf{j}=\left< 0,1,0\right>\) y \(\mathbf{k}=\left< 0,0,1\right>\) el producto escalar de cualquiera par de ellos es cero, los cual confirma la ilustración geométrica de que estos vectores son perpendiculares entre si y además, $$\mathbf{i}\cdot\mathbf{i}=\mathbf{j}\cdot\mathbf{j}=\mathbf{k}\cdot\mathbf{k}=1$$ que es la razón por lo cual no es necesario escribir los vectores \(\mathbf{i},\ \mathbf{j},\mathbf{k}\) al realizar el producto escalar.
Ver el ejercicio Ej2 y Ej3 del apartado Ejecicios II en la parte superior.
Producto vectorial.
Sean los vectores \( \mathbf{\vec{u}}=u_x\mathbf{i}+u_y\mathbf{j}+u_z\mathbf{k}~~{\rm y}~~ \mathbf{\vec{v}}=v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k}\) tales que \(\phi\) es el ángulo entre ellos, el producto vectorial de \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) denotado como \(\mathbf{\vec{u}}\times\mathbf{\vec{v}}\), también llamado producto cruz por su notación, es un nuevo vector el cual es ortogonal (normal) tanto a \(\mathbf{\vec{u}}\) como a \(\mathbf{\vec{v}}\) definido como,
Definición de producto vectorial.
$$\mathbf{\vec{u}}\times\mathbf{\vec{v}}=(u_2v_3-u_3v_2)\mathbf{i}+(u_1v_3-u_3v_1)\mathbf{j}+(u_1v_2-u_2v_1)\mathbf{k}$$
Al aplicar esta definición a los vectores canónicos \(\mathbf{i},\mathbf{j},\ \mathbf{k}\) se obtiene;
\begin{array}{l}
\mathbf{i}\times\mathbf{i}=\mathbf{0}& \mathbf{j}\times\mathbf{j}=\mathbf{0}& \mathbf{k}\times\mathbf{k}=\mathbf{0}\\
\mathbf{i}\times\mathbf{j}=\mathbf{k}& \mathbf{j}\times\mathbf{k}=\mathbf{i}& \mathbf{k}\times\mathbf{i}=\mathbf{j}\\
\mathbf{i}\times\mathbf{k}=-\mathbf{j}& \mathbf{k}\times\mathbf{j}=-\mathbf{i}& \mathbf{j}\times\mathbf{i}=-\mathbf{k}
\end{array}
Se pueden recordar estos resultados al considerar el producto vectorial de los vectores canónicos en un círculo el cual puede ser recorrido en sentido antihorario u horario. Cuando se recorre el círculo en sentido antihorario se obtienen los primeros tres resultados, así \(\mathbf{i}\times\mathbf{j}=\mathbf{k}\), cuando es en sentido horario entonces se tiene los negativos, \(\mathbf{i}\times\mathbf{k}=-\mathbf{j}\) (va para atrás).
Denotando el vector \(\mathbf{\vec{u}}\times\mathbf{\vec{v}}=\mathbf{\vec{r}}\) el módulo del vector entonces el módulo del vector \(\mathbf{\vec{r}}\) está dado por \(\mathbf{\vec{r}}=||\mathbf{\vec{u}}||||\mathbf{\vec{v}}||\sin{ϕ}\). Además, para un vector unitario \(\hat{r}\) normal al plano que contine los vectores \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) es posible escribir, $$\mathbf{\vec{r}}=||\mathbf{\vec{u}}||||\mathbf{\vec{v}}||\sin{ϕ} \mathbf{\hat{r}}$$
En la práctica es más simple recordar la definición de producto vectorial al considerar su forma alternativa como un determinante.
Definición alternativa del producto vectorial.
Sean los vectores \(\mathbf{\vec{u}}=\left< u_1,u_2,u_3\right>\) y \( \mathbf{\vec{v}}=\left< v_1,v_2,v_3\right>\) que también pueden escribirse en función de los vectores unitarios \(\mathbf{i},\mathbf{j},\mathbf{k},\) como, \begin{align} \mathbf{\vec{u}}=&u_1\mathbf{i}+u_2\mathbf{j}+u_3\mathbf{k}\\ \mathbf{\vec{v}}=&v_1\mathbf{i}+v_2\mathbf{j}+v_3\mathbf{k} \end{align} entonces el producto vectorial \(\mathbf{\vec{u}}\times\mathbf{\vec{v}}\) es, $$\mathbf{\vec{u}}\times\mathbf{\vec{v}}=\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\u_1&u_2&u_3\\v_1&v_2&v_3\\\end{matrix}\right|=\left|\begin{matrix}u_2&u_3\\v_2&v_3\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}u_1&u_3\\v_1&v_3\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}u_1&u_2\\v_1&v_2\\\end{matrix}\right|\mathbf{k}$$
Se debe notar que en sentido estricto esta expresión no es un determinante, ya que los elementos del primer renglón (fila) son vectores y no números, sin embargo, obviando este detalle es muyo más fácil realizar el producto cruz de dos vectores. Otro elemento importante es recordar que a diferencia del producto escalar el producto cruz es un vector no un número.
Se tienen muchas aplicaciones del producto vectorial tanto en matemática como en ciencias físicas. Algunas cantidades físicas de naturaleza vectorial se explican analíticamente por medio de este producto y en el campo de las matemáticas se pueden describir áreas y volúmenes de manera simple, este hecho se ilustra a continuación en los ejemplos siguientes.
Ejemplo. Momento de torsión. el momento de torsión \(\vec{\mathbf{\tau}}\) (tau) también llamado vector torca, par de torsión o momento de fuerza es un vector el cual “describe” el movimiento de un cuerpo que girar sobre un eje fijo, y
mediante la expresión, $$\vec{\mathbf{\tau}}=\vec{\mathbf{r}}\times\vec{\mathbf{F}}.$$
Se aplica una fuerza \(\vec{\mathbf{F}}=\left(3.0\hat{\mathbf{i}}+5.0\hat{\mathbf{j}}\right)N\) sobre un objeto el cual puede girar en torno a un eje fijo en la dirección del eje \(z.\) Si la fuerza se aplica en un punto cuya ubicación es, \(
\vec{\mathbf{r}}\left(7.0\hat{\mathbf{i}}+7.0\hat{\mathbf{j}}\right)m\) determinar la magnitud del vector momento de torsión.
Solución: la magnitud del vector torca es \(||\vec{\mathbf{\tau}}||=\sqrt{\tau_x^2+\tau_y^2+\tau_z^2}.\) Para
hallar las componentes se realiza el producto cruz.
\begin{align}
\mathbf{\tau}=&\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\7.0&7.0&0.0\\3.0&5.0&0.0\\\end{matrix}\right|=\left|\begin{matrix}7.0&0.0\\5.0&0.0\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}7.0&0.0\\3.0&5.0\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}7.0&7.0\\3.0&5.0\\\end{matrix}\right|\mathbf{k}\\
\mathbf{\tau}=&\left(35-21\right)\mathbf{k}=14\mathbf{k}Nm\\
\left|\left|\mathbf{\tau}\right|\right|=&\sqrt{\left(14Nm\right)^2}=14Nm
\end{align}
Ejemplo. Fuerza magnética. La fuerza magnética (medida en tesla T) a la cual es sometida un cuerpo está dada por $$\vec{\mathbf{F}}=q\mathbf{v}\times\mathbf{B}$$
donde \(q\) es la carga, \(\vec{\mathbf{v}}\) es el vector velocidad y \(\mathbf{B}\) es el vector de campo magnético. Un protón se mueve con una velocidad \(\mathbf{v}=(3\mathbf{i}\ – 4j + 2k) m/s\) en una región donde el campo magnético es \(\mathbf{B}=(5\mathbf{i}\ +\ 2\mathbf{j}\ – 3k) T.\) ¿Cuál es la magnitud de la fuerza magnética que experimenta esta carga?
Solución: la magnitud de la fuerza está dada por \( ||\vec{\mathbf{F}}||=qv×B\) donde \(q=1.60\times{10}^{-19}C\) es la carga del protón.
\begin{align}
\mathbf{v}\times\mathbf{B}=&\left|\begin{matrix}\mathbf{i}&\ \ \ \ \mathbf{j}&\ \ \ \mathbf{k}\\3&-4&\ \ \ 2\\5&\ \ \ 2&-3\\\end{matrix}\right|=\left|\begin{matrix}-4&\ \ 2\\2&-3\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}3&\ \ 2\\5&-3\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}3&-4\\5&\ \ \ \ 2\\\end{matrix}\right|\mathbf{k}\\
\mathbf{v}\times\mathbf{B}=&(8\mathbf{i}+19\mathbf{j}+26\mathbf{k})T m/s\\
||\mathbf{v}\times\mathbf{B}||=&\sqrt{8^2+19^2+26^2}=\sqrt{1101}Tms\\
F=&qv×B=1.60×10^{-19}C \sqrt{1101}Tms\\
F=&5.31\times{10}^{-18}N
\end{align}
Ejemplo. Área de un paralelogramo. El área de un paralelogramo en unidades cuadradas \((u^2),\) cuyos lados adyacentes son los vectores \(\mathbf{u}\) y \(\mathbf{v}\) está dada por $$A=||\mathbf{u}\times\mathbf{v}||$$
Determinar el área del paralelogramo de lados adyacentes \(\mathbf{u}=(2\mathbf{i}\ +\ 2\mathbf{j}\ – 4k)\) y \(\mathbf{v}=(-2\mathbf{i}\ +3\mathbf{j}\ +\ 4\mathbf{k})\)
\begin{align}
\mathbf{u}\times\mathbf{v}=&\left|\begin{matrix}\ \ \ \mathbf{i}&\mathbf{j}&\ \ \ \mathbf{k}\\\ \ \ 2&2&-4\\-2&3&\ \ \ 4\\\end{matrix}\right|=\left|\begin{matrix}2&-4\\3&\ \ \ 4\\\end{matrix}\right|\mathbf{i}-\left|\begin{matrix}\ \ \ 2&-4\\-2&\ \ \ 4\\\end{matrix}\right|\mathbf{j}+\left|\begin{matrix}\ \ \ 2&2\\-2&3\\\end{matrix}\right|\mathbf{k}\\
\mathbf{u}\times\mathbf{v}=&20\mathbf{i}+10\mathbf{k}\\
A=&\left|\left|\mathbf{u}\times\mathbf{v}\right|\right|\\
A=&\sqrt{{20}^2+{10}^2}=\sqrt{500}u^2
\end{align}
Como puede notar existen diversas aplicaciones para un determinante de orden \(3\times3\) estos son solo algunos de los múltiples ejemplos que puede encontrar al estudiar física o matemáticas. Aun queda mucho por conocer.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Dados los puntos los puntos \(P\left(2,\ 3,\ 5\right)\) y \(Q(8,6,10)\) determinar los vectores \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) que van desde \(P\) a \(Q\) y desde \(Q\) hasta \(P\) respectivamente, al junto de sus módulos.
Vectores unitarios. Determinar los vectores unitarios en la dirección del vector dado. $$ a.~\mathbf{\vec{v}}_1=\left< 3,5,7\right>~~~~~b.~\mathbf{\vec{v}}_2 =\left< 3,0,4\right>~~~~~c.~\mathbf{\vec{v}}_3 =\left< 3\sin{t},0,-3\cos{t}\right>$$
Un vector de un módulo dado. Determinar un vector de módulo tres, en la dirección de \({\mathbf{\vec{v}}}=\left< 7,5,26\right>\)
Determinar la suma de los vectores \(\mathbf{\vec{u}}=10.0m\) a \(120°\) con el este (referencia estándar) y \(\mathbf{\vec{v}}=20.0m\) a \(45.0°\) con el Este, por el método del triángulo.
Ángulos directores. Determinar los ángulos directores del vector \( \mathbf{\vec{r}}=3\mathbf{i}+5\mathbf{j}+7\mathbf{k}.\)
Adición de vectores por componentes. Dados los vectores \(\mathbf{\vec{u}}=\left< 3,4\right>\) y \(\mathbf{\vec{v}}=\left< -2,-1\right>\) determinar \(\mathbf{\vec{r}}=\mathbf{\vec{u}}+3\mathbf{\vec{v}}.\)
Adició de vectores por componentes. Dado el vector \(\mathbf{\vec{u}}= 3\mathbf{i}+4\mathbf{j}-5\mathbf{k}\) y el vector \(\mathbf{\vec{v}}=4\mathbf{i}-2\mathbf{k}\) determinar el módulo del vector \(\mathbf{\vec{r}}=2\mathbf{\vec{u}}+5\mathbf{\vec{v}}.\)
Adicion de vectores por componentes. Dada la figura de la izquierda (dibujo no está a escala), donde \(A=20.0m,~ B=22.0m,~C=15.0m,\) \(\beta_1={30.0°},\) \(\beta_2={35.0°}\) y \(\beta_3=40.0°\) determinar la suma de los vectores en cada caso. \begin{align} 1.&~~\mathbf{\vec{u}}=\mathbf{\vec{A}}+3\mathbf{\vec{B}}\\ 2.&~~\mathbf{\vec{v}}=2\mathbf{\vec{A}}-5\mathbf{\vec{C}} \end{align}
Ejemplo. Determinar el módulo y dirección del vector \(\mathbf{\vec{r}}=\mathbf{\vec{u}}+\mathbf{\vec{v}}\) dados los vectores \(\mathbf{\vec{u}}=10.0m\) a \(120°\) con el este y \(\mathbf{\vec{v}}=20.0m\) a \(45.0°\) con el Este.
Aceleración de un cuerpo. Un cuerpo de masa \(m=20{\rm kg}\) es sometido a tres fuerzas tal que \(\mathbf{\vec{F}}_1=3.0\mathbf{i}+9.0\mathbf{j}+2.0\mathbf{k},\) \(\mathbf{\vec{F}}_2=6.0\mathbf{i}+7.0\mathbf{j}-3.0\mathbf{k}\) y \(\mathbf{\vec{F}}_3=5.0\mathbf{i}+7.0\mathbf{j}+5.0\mathbf{k}\) donde las fuerzas se miden en newton. Determinar la aceleración \(\mathbf{\vec{a}}\) que es sometido y su magnitud, sabiendo que si la masa es \(m=cte\) entonces \(\sum\mathbf{\vec{F}}=m\mathbf{\vec{a}}\)
Producto escalar de vectores. Determinar el producto escalar de los vectores dados. \begin{align} a.\ \mathbf{\vec{u}}&=\left< 7,11\right> ~{\rm y} ~\mathbf{\vec{v}}=\left< 3,9\right>\\ b.\ \mathbf{\vec{u}}&=\left< 5,7,11\right>~ {\rm y}~ \mathbf{\vec{v}}=\left< -2,0,-3\right> \end{align}
Ángulo entre dos vectores. Determinar el ángulo entre los vectores dados para cada situación. \begin{align} \mathbf{\vec{u}}&=\left< 2,3,5\right> {\rm ~~y~~} \vec{\mathbf{v}}=\left< 3,4,7\right>\\ \mathbf{\vec{u}}&=\left< 2,3,0\right> {\rm ~~y~~} \vec{\mathbf{v}}=\left< 7,5,0\right>\\ \mathbf{i}&=\left< 1,0,0\right> {\rm ~~y~~} \mathbf{k}=\left< 0,0,1\right>\\ \end{align}
Condición de perpendicularidad. Determinar si los vectores dados son o no ortogonales. \begin{align} \mathbf{\vec{u}}&=3\mathbf{i}\ –4j+2k {~~\rm y~~} \vec{\mathbf{v}}=5\mathbf{i}\ +\ 2\mathbf{j}\ –3k\\ \mathbf{\vec{u}}&=8\mathbf{i}+19\mathbf{j}+26\mathbf{k} {~~\rm y~~} \mathbf{\vec{v}}=5\mathbf{i}+\ 2\mathbf{j}\ –3k\\ \mathbf{\vec{u}}&=7\mathbf{k} {~~\rm y~~} \vec{\mathbf{v}}=11\mathbf{i}\\ \end{align}
Producto vectorial sin uso de determinante. Dados los vectores \(\mathbf{\vec{u}}=3\mathbf{i} – 4\mathbf{j} + 2\mathbf{k}\) y \(\mathbf{\vec{v}}=5\mathbf{i}\ + 2\mathbf{j} – 3\mathbf{k}\) determinar el producto vectorial \(\mathbf{\vec{u}}\times\mathbf{\vec{v}}.\)
Dados los vectores \(\mathbf{\vec{u}}=(3\mathbf{i}–4\mathbf{j}+2\mathbf{k})\) y \(\mathbf{\vec{v}}=(5\mathbf{i}+2\mathbf{j}–3\mathbf{k})\) determinar el vector \(\mathbf{\vec{r}}=\mathbf{\vec{u}}\times\mathbf{\vec{v}}\) aplicando determinantes.
Momento de torsión. El momento de torsión \(\vec{\mathbf{\tau}}\) (tau) también llamado vector torca, par de torsión o momento de fuerza, es un vector el cual “describe” el movimiento de un cuerpo que gira sobre un eje fijo, expresado matemáticamente como $$\mathbf{\vec{\tau}}=\mathbf{\vec{r}}\times\mathbf{\vec{F}}.$$ Se aplica una fuerza \(\vec{\mathbf{F}}=\left(3.0\mathbf{i}+5.0\mathbf{j}\right)\)N sobre un objeto el cual puede girar en torno a un eje fijo en la dirección del eje \(z\). Si la fuerza se aplica en un punto cuya ubicación es \(\mathbf{\vec{r}}=\left(7.0\mathbf{i}+7.0\mathbf{j}\right)m\) determinar la magnitud del vector torca \(\mathbf{\vec{\tau}}\).
La fuerza magnética \(\mathbf{\vec{F}}\) (medida en tesla T) a la cual es sometida una carga \(q\) está dada, por \(\mathbf{\vec{F}}=q\mathbf{\vec{v}}\times\mathbf{\vec{B}},\) donde \(\mathbf{\vec{v}}\) es el vector velocidad y \(\mathbf{\vec{B}}\) es el vector de campo magnético. Un electrón se mueve con una velocidad \(\mathbf{\vec{v}}=(3\mathbf{i}–4\mathbf{j}+2\mathbf{k})ms\) en una región donde el campo magnético es \(\mathbf{\vec{B}}=(5\mathbf{i}\ +2\mathbf{j}–3\mathbf{k})T.\) ¿Cuál es la magnitud (en newton N) de la fuerza \(\mathbf{\vec{F}}\) que experimenta esta carga?
Área de un paralelogramo. Determinar el área del paralelogramo de lados adyacentes \(\mathbf{\vec{u}}=2\mathbf{i}\ +2\mathbf{j}– 4\mathbf{k}\) y \(\mathbf{\vec{v}}=-2\mathbf{i}\ +3\mathbf{j}+4\mathbf{k}\), si se sabe que el área del paralelogramo (en unidades cuadradas), cuyos lados adyacentes son los vectores \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) está dada por \( A=||\mathbf{\vec{u}}\times\mathbf{\vec{v}}||\)